Bayesian Risk and the Internment of Japanese Americans

We can use Bayes (see previous post) to model the US government’s decision to incarcerate Japanese Americans, 80,000 of which were US citizens, to reduce a perceived security risk. We can then use a quantified risk model to evaluate the internment decision.

We define two primary hypotheses regarding the loyalty of Japanese Americans:

• H1: The population of Japanese Americans are generally loyal to the United States and collectively pose no significant security threat.
  
  
• H2: The population of Japanese Americans poses a significant security threat (e.g., potential for espionage or sabotage).

The decision to incarceration Japanese Americans reflects policymakers’ belief in H2 over H1, updated based on evidence like the Niihau Incident.

Prior Probabilities

Before the Niihau Incident, policymakers’ priors were influenced by several factors:

• Historical Context: Anti-Asian sentiment on the West Coast, including the 1907 Gentlemen’s Agreement and 1924 Immigration Act, fostered distrust of Japanese Americans.
  
  
• Pearl Harbor: The surprise attack on December 7, 1941, heightened fears of internal threats. No prior evidence of disloyalty existed.
  
  
• Lack of Data: No acts of sabotage or espionage by Japanese Americans had been documented before Niihau. Espionage detection and surveillance were limited. Several espionage rings tied to Japanese nationals were active (Itaru Tachibana, Takeo Yoshikawa).

Given this, we can estimate subjective priors:

• P(H1) = 0.99: Policymakers might have initially been 99 percent confident that Japanese Americans were loyal, as they were U.S. citizens or long-term residents with no prior evidence of disloyalty. The pre-Pearl Harbor Munson Report (“There is no Japanese `problem’ on the Coast”) supported this belief.
  
  
• P(H2) = 0.01: A minority probability of threat due to racial prejudices, fear of “fifth column” activities, and Japan’s aggression.

These priors are subjective and reflect the mix of rational assessment and bias prevalent at the time. Bayesian reasoning (Subjective Bayes) requires such subjective starting points, which are sometimes critical to the outcome.

Evidence and Likelihoods

The key evidence influencing the internment decision was the Niihau Incident (E1) modeled in my previous post. We focus on this, as it was explicitly cited in justifying internment, though other factors (e.g., other Pearl Harbor details, intelligence reports) played a role.

E1: The Niihau Incident

Yoshio and Irene Harada, Nisei residents, aided Nishikaichi in attempting to destroy his plane, burn papers, and take hostages. This was interpreted by some (e.g., Lt. C.B. Baldwin in a Navy report) as evidence that Japanese Americans might side with Japan in a crisis.

Likelihoods:

P(E1|H1) = 0.01: If Japanese Americans are generally loyal, the likelihood of two individuals aiding an enemy pilot is low. The Haradas’ actions could be seen as an outlier, driven by personal or situational factors (e.g., coercion, cultural affinity). Note that this 1% probability is not the same 1% probability of H1, the prior belief that Japanese Americans weren’t loyal. Instead, P(E1|H1) is the likelihood assigned to whether E1, the Harada event, would have occurred given than Japanese Americans were loyal to the US.

P(E1|H2) = 0.6: High likelihood of observing the Harada evidence if the population of Japanese Americans posed a threat.

Posterior Calculation Using Bayes Theorem:

P(H1∣E1) = P(E1∣H1)⋅P(H1) / [P(E1∣H1)⋅P(H1)+P(E1∣H2)⋅P(H2)]

P(H1∣E1)=0.01⋅0.99 / [(0.01⋅0.99)+(0.6⋅0.01)] = 0.626

P(H2|E1) = 1 – P(H1|E1) = 0.374

The Niihau Incident significantly increases the probability of H2 (its prior was 0.01), suggesting a high perceived threat. This aligns with the heightened alarm in military and government circles post-Niihau. 62.6% confidence in loyalty is unacceptable by any standards. We should experiment with different priors.

Uncertainty Quantification

• Aleatoric Uncertainty: The Niihau Incident involved only two people.
  
  
• Epistemic Uncertainty: Prejudices and wartime fear would amplify P(H2).

Sensitivity to P(H1)

The posterior probability of H2 is highly sensitive to changes in P(H2) – and to P(H1) because they are linearly related: P(H2) = 1.0 – P(H1).

The posterior probability of H2 is somewhat sensitive to the likelihood assigned to P(E1|H1), but in a way that may be counterintuitive – because it is the likelihood assigned to whether E1, the Harada event, would have occurred given than Japanese Americans were loyal. We now know them to have been loyal, but that knowledge can’t be used in this analysis. Increasing this value lowers the posterior probability.

The posterior probability of H2 is relatively insensitive to changes in P(E1|H2), the likelihood of observing the evidence if Japanese Americans posed a threat (which, again, we now know them to have not).

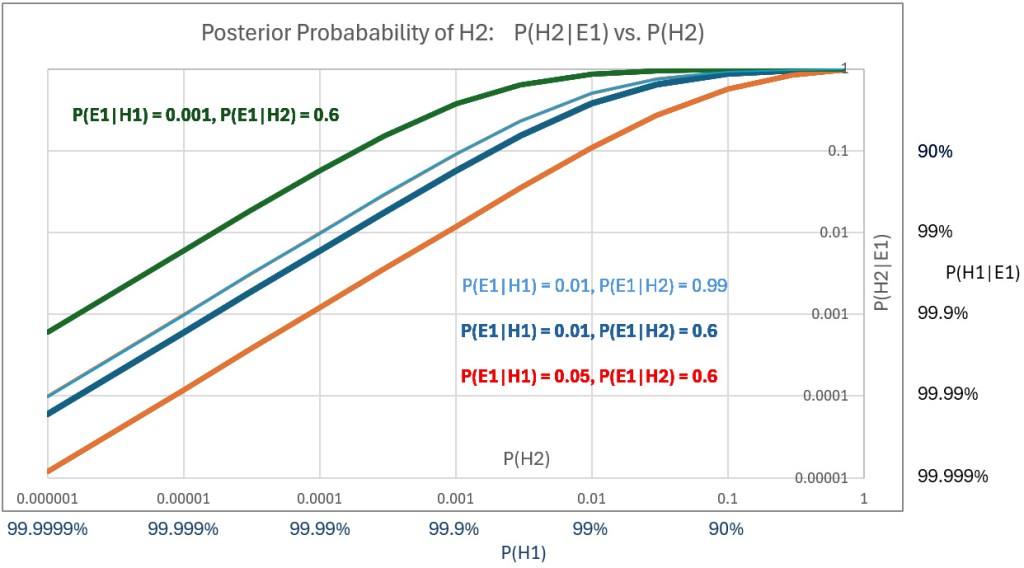
A plot of posterior probability of H2 against the prior probabilities assigned to H2 – that is, P(H2|E1) vs P(H2) – for a range of values of P(H2) using three different values of P(E1|H1) shows the sensitivities. The below plot (scales are log-log) also shows the effect of varying P(E1|H2); compare the thin blue line to the thick blue line.

Prior hypotheses with probabilities greater the 99% represent confidence levels that are rarely justified. Nevertheless, we plot high posteriors for priors of H1 (i.e., posteriors of H2 down to 0.00001 (1E-5). Using P(E1|H1) = 0.05 and P(E1|H2 = 0.6, we get a posterior P(H2|E1) = 0.0001 – or P(H1|E1) = 99.99%, which might be initially judged as not supporting incarceration of US citizens in what were effectively concentration camps.

Risk

While there is no evidence of either explicit Bayesian reasoning or risk quantification by Franklin D. Roosevelt or military analysts, we can examine their decisions using reasonable ranges of numerical values that would have been used if numerical analysis had been employed.

We can model risk, as is common in military analysis, by defining it as the product of severity and probability – probability equal to that calculated as the posterior probability that a threat existed in the population of 120,000 who were interned.

Having established a range of probabilities for threat events above, we can now estimate severity – the cost of a loss – based on lost lives and lost defense capability resulting from a threat brought to life.

The Pearl Harbor attack itself tells us what a potential hazard might look like. Eight U.S. Navy battleships were at Pearl Harbor: Arizona, Oklahoma, West Virginia, California, Nevada, Tennessee, Maryland, and Pennsylvania. Typical peacetime crew sizes ranged from 1,200 to 1,500 per battleship, though wartime complements could exceed that. About 8,000–10,000 sailors were assigned to the battleships. More sailors would have been on board had the attack not happened on a Sunday morning.

About 37,000 Navy and 14,000 Army personnel were stationed at Pearl Harbor. 2,403 were killed in the attack, most of them aboard battleships. Four battleships were sunk. The Arizona suffered a catastrophic magazine explosion from a direct bomb hit. Over 1,170 crew members were killed. 400 were killed on the Oklahoma when it sank. None of the three aircraft carriers of the Pacific Fleet were in Pearl Harbor on Dec. 7. The USS Enterprise was due to be in port on Dec. 6 but was delayed by weather. Its crew was about 2,300 men.

Had circumstances differed slightly, the attack would not have been a surprise, and casualties would have been fewer. But in other conceivable turns of events, they could have been far greater. A modern impact analysis of an attack on Pearl Harbor or other bases would consider an invasion’s “cost” to be 10 to 20,000 lives and the loss of defense capability due to destroyed ships and aircraft. Better weather could have meant destruction of one third of US aircraft carriers in the Pacific.

Using a linear risk model, an analyst, if such analysis was done back then, might have used the above calculated P(H2|E1) as the probability of loss and 10,000 lives as one cost of the espionage. Using probability P(H1) in the range of 99.99% confidence in loyalty – i.e., P(H2) = 1E-4 – and severity = 10,000 lives yields quantified risk.

As a 1941 risk analyst, you would be considering a one-in-10,000 chance of losing 10,000 lives and loss of maybe 25% of US defense capacity. Another view of the risk would be that each of 120,000 Japanese Americans poses a one-in-10,000 chance of causing 10,000 deaths, an expected cost of roughly 120,000 lives (roughly, because the math isn’t quite as direct as it looks in this example).

While I’ve modeled the decision using a linear expected value approach, it’s important to note that real-world policy, especially in safety-critical domains, is rarely risk-neutral. For instance, Federal Aviation Regulation AC 25.1309 states that “no single failure, regardless of probability, shall result in a catastrophic condition”, a clear example of a threshold risk model overriding probabilistic reasoning. In national defense or public safety, similar thinking applies. A leader might deem a one-in-10,000 chance of catastrophic loss (say, 10,000 deaths and 25% loss of Pacific Fleet capability) intolerable, even if the expected value (loss) were only one life. This is not strictly about math; it reflects public psychology and political reality. A risk-averse or ambiguity-intolerant government could rationally act under such assumptions.

Would you take that risk, or would you incarcerate? Would your answer change if you used P(H1) = 99.999 percent? Could a prior of that magnitude ever be justified?

From the perspective of quantified risk analysis (as laid out in documents like FAR AC 25.1309), President Roosevelt, acting in early 1942 would have been justified even if P(H1) had been 99.999%.

In a society so loudly committed to consequentialist reasoning, this choice ought to seem defensible. That it doesn’t may reveal more about our moral bookkeeping than about Roosevelt’s logic. Racism existed in California in 1941, but it unlikely increased scrutiny by spy watchers. The fact that prejudice existed does not bear on the decision, because the prejudice did not motivate any action that would have born – beyond the Munson Report – on the prior probabilities used. That the Japanese Americans were held far too long is irrelevant to Roosevelt’s decision.

Since the rationality of Roosevelt’s decision, as modeled by Bayesian reasoning and quantified risk, ultimately hinges on P(H1), and since H1’s primary input was the Munson Report, we might scrutinize the way the Munson Report informs H1.

The Munson Report is often summarized with its most quoted line: “There is no Japanese ‘problem’ on the Coast.” And that was indeed its primary conclusion. Munson found Japanese American citizens broadly loyal and recommended against mass incarceration. However, if we assume the report to be wholly credible – our only source of empirical grounding at the time – then certain passages remain relevant for establishing a prior. Munson warned of possible sabotage by Japanese nationals and acknowledged the existence of a few “fanatical” individuals willing to act violently on Japan’s behalf. He recommended federal control over Japanese-owned property and proposed using loyal Nisei to monitor potentially disloyal relatives. These were not the report’s focus, but they were part of it. Critics often accuse John Franklin Carter of distorting Munson’s message when advising Roosevelt. Carter’s motives are beside the point. Whether his selective quotations were the product of prejudice or caution, the statements he cited were in the report. Even if we accept Munson’s assessment in full – affirming the loyalty of Japanese American citizens and acknowledging only rare threats – the two qualifiers Carter cited are enough to undercut extreme confidence. In modern Bayesian practice, priors above 99.999% are virtually unheard of, even in high-certainty domains like particle physics and medical diagnostics. From a decision-theoretic standpoint, Munson’s own language renders such priors unjustifiable. With confidence lower than that, Roosevelt made the rational decision – clear in its logic, devastating in its consequences.