Posts Tagged metallurgy
Climbing Taiwan Removable Bolts Review
Posted by Bill Storage in Engineering & Applied Physics on November 6, 2025
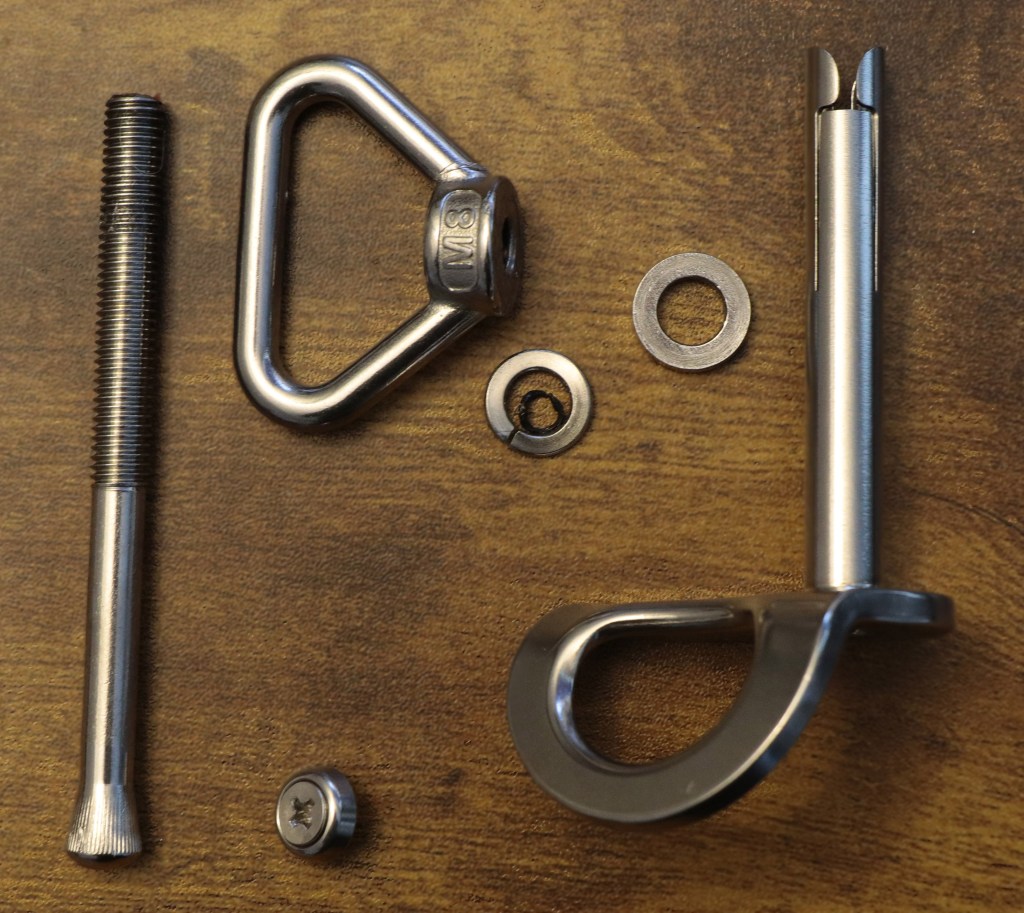
Friends and I have been experimenting with removable bolts in muddy caves, and many of us have been concerned about the robustness of the devices. I don’t mean their strength. They’re plenty strong. I mean how well do they hold up in a cave environment – and can we be ensured of a good placement. I just got some new removable bolts from Climbing Taiwan (CT). Compared to the Petzl Pulse design, which have proven to be finicky in caves, they look like they might be better suited for use in cave environments.
I don’t have a cave or a hammer drill on hand right now, so I put a 10mm masonry bit in my handheld driver and drilled holes in a concrete block to test the bolts.
For this testing I wanted to drill the hole barely long enough to fit the bolt in – against the recommendations of the manufacturer. I wanted to experiment with the consequences of crud in the bottom of the hole.
Normally, with 3/8 and 10mm bolts wedge bolts wedge bolts I don’t blow out the holes or brush them underground. I merely withdraw the drill with it rotating slightly and pull the dust out of the hole. I’ve placed hundreds of bolts and have never had a spinner. I torque my 3/8 wedge bolts to 25 foot pounds underground.
Because, for these tests, I am drilling vertically downward and I am using a masonry bit instead of a hammer drill bit, I had to brush the dust out of these holes. I did not use a blow tube. This is really bad bolting hygiene. I wanted to see if I could gum up the works. I am intentionally using these removable bolts wrong, against the advice of the manufacturer, and against good sense.
To simulate the abuse that bolts take underground, I first mixed the concrete dust with water and packed it onto the bolt mechanism. Then I poured the sludge into the hole.
Then I added sand to the mix. I packed on as much sand as I could. I also tried getting sand into the threads at the top of the hanger. This proved no problem for installation or removal. I then pushed sand into the hole to see if I could force the wedge through the sand sludge and back toward the outside of the hole.
For the next simulation of cave mud I combined honey and cornstarch. Wet corn starch is fun to use in these experiments because it is a non-euclidean fluid with some odd properties. I again added sand. I then smeared the cornstarch honey sand combination along the sleeve and the threaded region.
For the next test I got a fresh cylinder of clay- rich mud and added it to the mix. The bolt and the sludge clearly filled the entire hole as is visible by the overflow. I did the same with a mix of plumber’s grease and garden dirt. Again, no problem.
I used a pressure washer to clean them. I took them apart to be sure. Good as new.
The manufacturer says they used 2205 stainless steel for the threaded shaft and 304 for everything else. These are smart choices that reflect sound engineering. 304 is very widely used. It’s machinable and has high ductility. Its ultimate strength is several times higher than its yield strength. It is extremely forgiving and has excellent corrosion resistance. Duplex 2205 is much stronger, much more expensive, and has some trade-offs (like weldability), none of which are at all relevant to this usage.
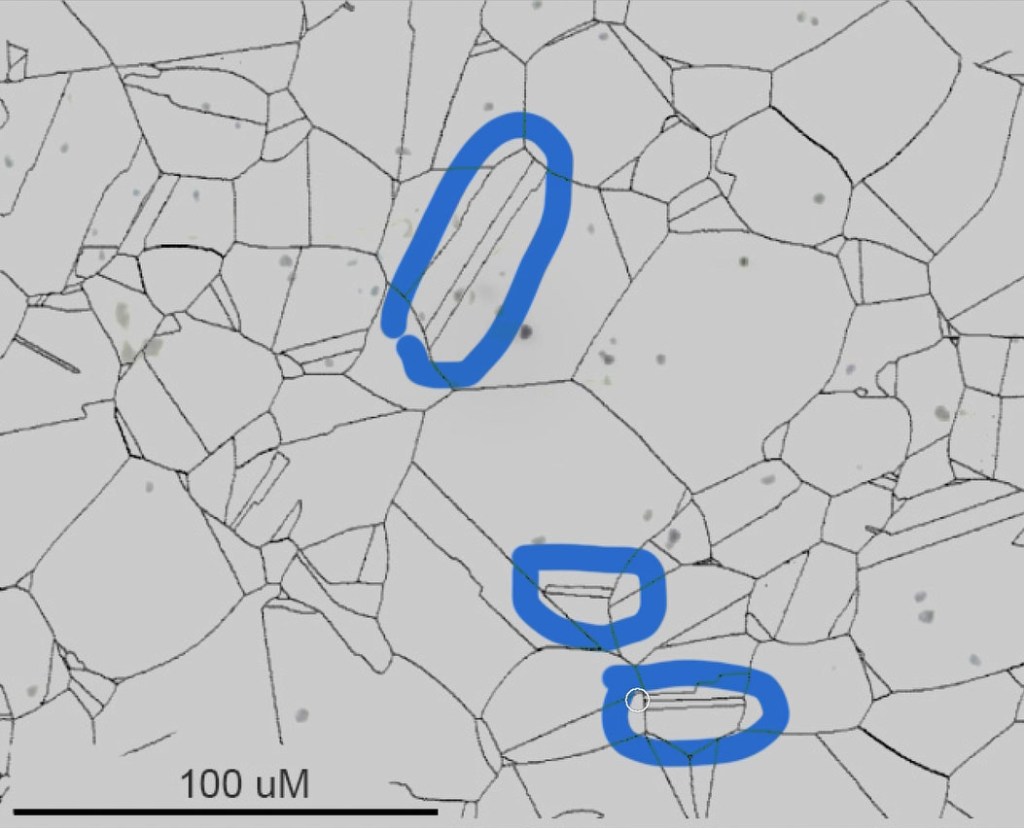
I tested the components for ferromagnetism. In theory, 304 alloy hangers should not be magnetic. OK, little bit of engineering here. 304 is austenitic; its atoms are arranged in a body-centered cubic structure. But when you cut or beat on austenitic stainless, you can cause some degree of room-temperature phase transformation. A room-temperature crystalline phase change always seemed like magic to me, but it happens. Ancient blacksmiths were similarly amazed. This cold-working causes atoms to jump into a body-centered tetragon pattern called martensite, which is magnetic. It also causes carbon atoms to bunch up a bit, and this can reduce corrosion life.
But these bolts are not intended as permanent anchors. And when I look at the hangers under a scope at 250x, I see maybe a couple of percent martensite. Rough calculation of the life of a 304 bolt in a typical Appalachian cave with no brine and low chlorides yields a range of about 1000 to 20,000 years. If we shift that bolt into its martensitic state, we’d reduce its life in a cave down to maybe 50 to 1,000 years. But that is for full martensite, and I’m seeing only a percent or two. In other words, we can ignore the fact that this hanger is slightly magnetic. The Duplex 2205 threaded shaft (“duplex” because it is part ferrite, part austenite – elongated austenite grains in a ferritic matrix, so it is magnetic), since it isn’t welded or otherwise altered, would have a corrosion life of 2 to 5 times that of 304.
I measured hardness at Rockwell C25 – around 90,000 psi – a bit higher than you’d expect for annealed 304, but consistent with the cold working that resulted in the magnetism. Totally inconsequential.
I generally don’t do destructive testing. It’s usually pointless or worse. It’s entertaining to watch gear break, but focusing on ultimate strength just encourages dangerous misconceptions. Safety in climbing gear depends on how forces are distributed, how materials deform, and, mostly, how elasticity affects the system – how energy is absorbed. The inelasticity of a static rope that’s stronger than a dynamic rope can kill you. F=ma and F=kx are not just equations – they are life-and-death considerations.
I like to look at the underlying physics, and highlight what matters in practical use. My goal is to give climbers accurate, responsible insight – not spectacle – and to counter the intuition that ‘stronger = safer.’ This approach is personal to me as well: a close friend died while aid climbing in a cave because he misunderstood these principles. We might honor his memory by helping others understand how stuff works.
Why not break them? The removable-bolt components – bolts and hangers – are made from standard engineering materials, like 304. These materials are mass-produced in sheet and rod form, and have extremely low likelihood of defects. 304 stainless is not a cottage-industry alloy. Producing it requires integrated melt, alloying, and forging infrastructure with tight control of composition and processing. You can’t fake it cheaply. So the global quality variation for 304 is extremely narrow compared to, say, low-alloy steels, bronze, or, unfortunately for cavers, aluminum castings and forgings. Counterfeit carabiners. But that’s another article.
Breaking these bolts on video would add zero real information. Their strength far exceeds what a human body can impose or withstand. What actually matters – the rock quality, technique, and proper installation – is rarely tested or demonstrated on YouTube. If there is concern about a manufacturer’s integrity, destructive testing of one or two bolts is meaningless. Instead, careful microstructural examination and non-destructive testing across a larger sample set provide meaningful insight, without teaching viewers some sort of cargo-cult science. Removable bolts are intended for shear loading only. Think standard aid climbs, not ones like this:
But any real-world usage involves some amount of axial load. Tests on other removable bolts show them to have very high strength in the axial direction. Usually, the rock blows out first.
The fact that the rock usually blows out first points to another advantage of these Climbing Taiwan bolts over the Petzl. In soft rock, bolt length trumps bolt diameter because rock strength dominates. The 3-inch, 10mm diameter CT bolt vs. the 2 and a quarter inch Petzl 12mm. In hard rock, bolt strength dominates, but in hard rock, the breaking strength for both 10 and 12mm far exceed survivability. This is a perfect example of where destructive testing results will lead you to the wrong conclusion.
With a few assumptions, we can easily calculate the relative performance of the Pulse and the CT bolts loaded in shear:
Sleeve / shaft sizes
- Pulse: sleeve Ø = 12.0 mm, shaft Ø = 10.0 mm, embed length = 55 mm
- CT (10 mm): sleeve Ø = 10.0 mm, shaft Ø = 8.0 mm, embed length = 77 mm.
- Material strengths (conservative working numbers)
- Sleeve material 304 stainless, UTS = 520 MPa. Shear strength = 0.6·UTS = 312 MPa.
- Shaft material 2205 duplex, UTS = 860 MPa. Shear strength = 0.6·UTS = 516 MPa.
- Use the shaft shear (2205) as the bolt shear limit.
- Two limiting modes considered, and the lower one governs:
For rock-limited shear:
Rock shear strength × lateral contact area of the sleeve (projected cylindrical area = π·d_sleeve·embed_length). This models shear/punching or interface shear of the sleeve against rock.
For bolt (shaft) shear:
Material shear strength × cross-sectional area of the shaft (π·d^2/4). This models a straight shear through the shaft.
No complex friction, bending, or stress concentrations included. This is a first-order, worst-case shear capacity comparison.
| Rock shear strength | Pulse 12 mm, embed 55 mm | CT 10 mm, embed 77 mm |
| 1000 psi | rock limit 14.30 kN (3,214 lb) bolt limit 40.53 kN (9,111 lb) | rock limit 16.68 kN (3,761 lb) bolt limit 25.94 kN (5,831 lb) |
| 2000 psi | rock limit 28.59 kN (6,428 lb) bolt limit 40.53 kN (9,111 lb) | rock limit 33.36 kN (7,523 lb) bolt limit 25.94 kN (5,831 lb) |
| 4000 psi | rock limit 57.18 kN (12,855 lb) bolt limit 40.53 kN (9,111 lb) | rock limit 66.71 kN (14,998 lb) bolt limit 25.94 kN (5,831 lb) |
To evaluate the sensitivity of this model to assumptions, we can make the following changes, aiming at higher conservatism:
- 2205 duplex shear taken as 0.5·UTS, i.e. 430 MPa.
- A conservative Rock-punching reduction factor of 0.6 applied to the nominal rock shear strength to model local failure modes, stress concentrations, and imperfect contact.
| Rock shear strength | Pulse 12 mm, embed 55 mm | CT 10 mm, embed 77 mm |
| 1000 psi | rock limit 8.58 kN (1,928 lb) bolt limit 33.77 kN (7,592 lb) | rock limit 10.01 kN (2,250 lb) bolt limit 21.61 kN (4,859 lb) |
| 2000 psi | rock limit 17.16 kN (3,857 lb) bolt limit 33.77 kN (7,592 lb) | rock limit 20.01 kN (4,499 lb)bolt limit 21.61 kN (4,859 lb) |
| 4000 psi | rock limit 34.31 kN (7,713 lb) bolt limit 33.77 kN (7,592 lb) | rock limit 40.03 kN (8,999 lb) bolt limit 21.61 kN (4,859 lb) |
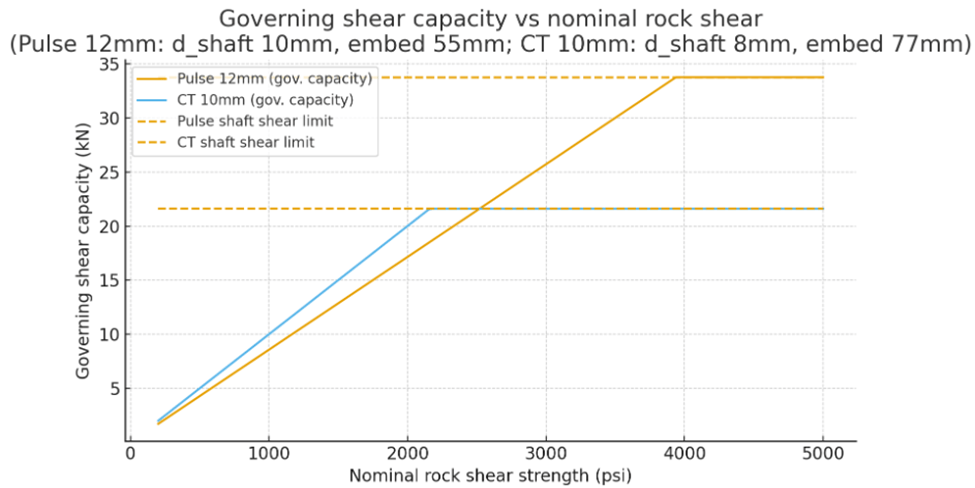
This results in lower strength values for both rock and bolt, but the relationships and conclusions still stand. In weak rock, length trumps diameter; in strong rock, bolt strength dominates but both 10 and 12mm strengths are far above survivability. The below chart plots governing capacity vs nominal rock shear to show the crossover points:
So my conclusion that the CT bolts are better designed for cave rock than the Petzl Pulses is not sensitive to assumptions about Rock-punching reduction factor or the relationship between 2205’s ultimate tensile and ultimate shear strength. The CT bolts come out looking like a better design for cave rock (and, of course, neither was designed for use in caves).
It’s also worth noting that the longer 10mm CT bolt removes 10 percent less rock than the shorter 12mm Petzl bolt. So you’re getting about 10% more bolting per battery.
Returning to axial strength. Because the core principle at work in these bolts is lateral expansion under confinement (a radial pressure multiplier from a low-angle taper), we need to control the hole diameter to achieve the needed confinement. These Climbing Taiwan bolts allow you to torque them down – in a sense. This isn’t torquing to achieve tensile preload, as in wedge anchors. It is about mechanically setting the wedge to the local bore diameter. Think of it like calibrating the anchor to the hole. You can expand the sleeve using the handle until you feel firm engagement. That lets you tune for real-world variability in hole diameter, rock roughness, or small flares and cracks. That seems to me the big advantage of this design; it’s more tolerant of the wobbly drilling that sub-optimal cave settings often give us.
Beyond being easier to clean and having superior strength in soft rock compared to the 12mm Petzl Pulse, the cleverness here is in better decoupling hole-fit adjustment from load resistance. I was able to engage the nominally 10mm bolt in a 12mm diameter hole. I’ll still avoid drilling bad holes, but this is very good to know, especially when drilling in confined or awkward places where suddenly the little Milwaukee decides to go on a rotary rampage.
If you have experience with these underground, or have questions or comments, please feel free to add a comment below. Sometimes I miss real engineering.
Unlocking the Secrets of Bulk Metallic Glass with Graph Computing
Posted by Bill Storage in Engineering & Applied Physics on June 24, 2025
This blog post was written in May 2022 by Amy Skowronski and Bill Storage for {Company}. {Company} did not accept it (or a shorter version) for publication because it was tangential to their current (at that time) focus. I’ll comment on that decision in a future post.
Fraud detection, drug discovery, and network security have all advanced with the help of graph computing – but these are just the early, obvious wins. The deeper promise of {Company}’s graph-native platform lies in uncovering complex relationships in domains most systems aren’t built to touch. To show what that looks like, we turn to a frontier yet revealing application: a class of advanced materials known as Bulk Metallic Glass.
Imagine a metal that’s stronger than steel, bends like plastic, and resists corrosion like glass. Bulk metallic glass (BMG), discovered in the 1960s, was found to have such characteristics. Recent advancements, enabled in part by high performance computing, give this revolutionary material the potential to transform industries from aerospace to medical devices.
Unlike the orderly atomic structures of common metals, BMGs boast a chaotic, amorphous arrangement that defies traditional metallurgy. At {Company}, we’re harnessing the power of graph computing to decode BMG’s atomic secrets, unlocking new possibilities for materials science. In this post, we’ll explore how BMGs differ from common metals and why graph analytics is the key to designing the next generation of advanced materials.
What Makes Bulk Metallic Glass So Special?
To understand BMGs, let’s start with the basics of metal structure. Most metals like steel and aluminum form crystalline lattices. These are highly organized, repeating patterns of atoms. The lattices define how metals behave: their strength, ductility, and even how they corrode. Common arrangements include:
- Face-Centered Cubic (FCC): Picture a cube with atoms at each corner and in the center of each face. This is most aluminum and copper. FCC metals are more ductile, ideal for shaping into wires or sheets.
- Body-Centered Cubic (BCC): Think of a cube with an atom at each corner and one in the center (e.g., iron at room temperature, which becomes FCC at higher temperatures). BCC metals are strong but less ductile, making them prone to brittle fracture under stress.
- Hexagon Close-Packed (HCP): Imagine tightly packed spheres stacked in a hexagonal pattern. This is most magnesium and titanium. HCP metals offer a balance of strength and formability, common in aerospace components.
All these structures are orderly, predictable, and rigid. But they have flaws – dislocations and grain boundaries where crystal regions meet. The boundaries act like seams, weaker than the surrounding fabric. Cracks and corrosion exploit the boundaries. Enter bulk metallic glass.
BMGs are amorphous; their atoms are arranged in a random, glass-like state, resembling a frozen liquid. Instead of lattices, BMG atoms are arranged in tightly packed clusters. This chaos gives BMGs unique properties:
- Incredible Strength: Without grain boundaries, BMGs resist cracking. Their strengths reach 2–3 GPa (300,000–400,000 psi), exceeding that of many high-strength steels, which typically top out around 1.5–2 GPa.
- Elasticity: BMGs can flex like polymers, deforming up to 2% before yielding, far exceeding the behavior of normal metals.
- Corrosion Resistance: Absence of ordered planes makes it harder for chemicals to attack and penetrate. BMGs are ideal for harsh environments like jet engines or implants.
- Processability: BMGs can be molded like glass when heated into their supercooled liquid region, enabling complex shapes for gears or biomedical stents.
Of course, there’s a catch, one that has hindered BMG development for decades. Designing BMGs is arduous. Their properties depend on precise compositions (e.g., Zr41.2Ti13.8Cu12.5Ni10Be22.5, known as Vitreloy 1) and extreme cooling rates in early systems (10⁵–10⁶ K/sec), though modern BMGs can form at rates as low as 1–100 K/sec. Understanding their atomic structure means solving a 3D puzzle with billions of pieces.
Graph Computing: Decoding BMG’s Atomic Chaos
BMGs’ amorphous structure is a network of atoms connected by bonds, with no repeating pattern. This makes them a perfect fit for graph analytics, where atoms are nodes and bonds are edges. {Company’s} high-performance graph platform can model these atomic networks at massive scale, revealing insights that traditional tools can’t touch. Here’s how it works:
1. Modeling the Amorphous Network
Imagine a BMG sample with billions of atoms, each bonded to 8–13 neighbors in a random cluster. {Company} represents this as a graph. Each node (atom) has properties like element type (e.g., Zr, Cu) and position. Each edge (bond) has attributes like bond strength or distance. Unlike crystalline metals, where lattices repeat predictably, BMG graphs are irregular, with varying degrees (number of bonds per atom) and clustering coefficients (how tightly atoms pack locally).
Using {Company’s} distributed graph engine, researchers can ingest terabytes of molecular dynamics (MD) simulation data – snapshots of atomic positions from supercomputers – and build these graphs in real time. Our platform’s ability to handle sparse, irregular graphs at scale (think 109 nodes and 1010 edges) makes it ideal for BMGs, outperforming traditional methods by 10–100x.
2. Analyzing Local Atomic Clusters
BMGs owe their strength to short-range order – local clusters like icosahedra (12 atoms around a central one) or tetrahedra (4 atoms tightly packed). These clusters don’t repeat globally but dominate locally, influencing properties like ductility. {Company’s} graph algorithms, like community detection (e.g., Louvain clustering), identify these motifs by finding densely connected subgraphs. For example, a high icosahedral cluster count in a Zr-based BMG correlates with better glass-forming ability and higher resistance to shear localization.
We also use graph neural networks (GNNs) to predict cluster stability. GNNs, using high-quality training data, learn from the graph’s topology and node features (e.g., atomic radii, electronegativity), predicting which compositions favor amorphous structures. This accelerates BMG design, reducing trial-and-error in the lab.
3. Simulating Defects and Dynamics
BMGs aren’t perfect. Shear transformation zones (STZs) – regions where atoms rearrange under stress – control their plasticity. {Company} models STZs as anomalous subgraphs, where nodes have unusual connectivity (e.g., lower or higher degree than average). Our anomaly detection algorithms can pinpoint these defects, helping engineers predict failure points.
Dynamic processes, like atomic rearrangements during cooling, are modeled as temporal graphs, where atom positions and inferred bonds change over time due to thermal motion or stress. {Company’s} real-time processing (powered by HPC roots) tracks these changes at scale, revealing how cooling rates affect amorphous stability. This is critical for scaling BMG production, because slow cooling often leads to unwanted crystallization.
4. Optimizing Composition
BMG recipes are complex, with 3–5 elements in precise ratios. {Company’s} graph traversal algorithms explore compositional spaces, identifying combinations that maximize icosahedral clusters or minimize crystallization risk. For instance, adding 1% Be to a Zr-Cu alloy can stabilize the amorphous phase. Our platform integrates with machine learning pipelines, enabling researchers to iterate faster than ever.
Why BMG Matters to Industry
BMGs are already making waves:
- Aerospace: NASA’s BMG gears for Mars rovers (developed and tested, not production to our knowledge) are 2x stronger than titanium, with no grain boundaries to fail under stress.
- Medical Devices: BMG implants resist corrosion in the body, lasting longer than the best stainless steels.
- Electronics: BMG casings for smartphones (e.g., Apple’s trials) combine strength with moldability for sleek designs.
The Future of Materials Science with {Company}
The global advanced materials market is projected to hit $1.1 trillion by 2027, and BMGs are a growing slice. But their potential is untapped due to design complexity. {Company’s} graph platform bridges this gap, enabling researchers to model, analyze, and optimize BMG structures at unprecedented scale. {Company’s} graph computing platform, with its roots in high-performance computing and expertise in Graph AI, is the perfect partner for this journey.
The Multidisciplinarian 
Recent Comments