Posts Tagged quantified risk
“He Tied His Lace” – Rum, Grenades and Bayesian Reasoning in Peaky Blinders
Posted by Bill Storage in Probability and Risk on August 4, 2025
“He tied his lace.” Spoken by a jittery subordinate halfway through a confrontation, the line turns a scene in Peaky Blinders from stylized gangster drama into a live demonstration of Bayesian belief update. The scene is a tightly written jewel of deadpan absurdity.
(The video clip and a script excerpt from Season 2, Episode 6 appears at the bottom of this article – rough language. “Peaky blinders,” for what its worth, refers to young brits in blindingly dapper duds and peaked caps in the 1920s.)
The setup: Alfie Solomons has temporarily switched his alliance from Tommy Shelby to Darby Sabini, a rival Italian gangster, in exchange for his bookies being allowed at the Epsom Races. Alfie then betrayed Tommy by setting up Tommy’s brother Arthur and having him arrested for murder. But Sabini broke his promise to Alfie, causing Alfie to seek a new deal with Tommy. Now Tommy offers 20% of his bookie business. Alfie wants 100%. In the ensuing disagreement, Alfie’s man Ollie threatens to shoot Tommy unless Alfie’s terms are met.
Tommy then offers up a preposterous threat. He claims to have planted a grenade and wired it to explode if he doesn’t walk out the door by 7pm. The lynchpin of this claim? That he bent down to tie his shoe on the way in, thereby concealing his planting the grenade among Alfie’s highly flammable bootleg rum kegs. Ollie falls apart when, during the negotiations, he recalls seeing Tommy tie his shoe on the way in. “He tied his lace,” he mutters frantically.
In another setting, this might be just a throwaway line. But here, it’s the final evidence given in a series of Bayesian belief updates – an ambiguous detail that forces a final shift in belief. This is classic Bayesian decision theory with sequential Bayesian inference, dynamic belief updates, and cost asymmetry. Agents updates their subjective probability (posterior) based on new evidence and choose an action to maximize expected utility.
By the end of the negotiation, Alfie’s offering a compromise. What changes is not the balance of lethality or legality, but this sequence of increasingly credible signals that Tommy might just carry through on the threat in response to Alfie’s demands.
As evidence accumulates – some verbal, some circumstantial – Alfie revises his belief, lowers his demands, and eventually accepts a deal that reflects the posterior probability that Tommy is telling the truth. It’s Bayesian updating with combustible rum, thick Cockney accents, and death threats delivered with stony precision.
Bayesian belief updating involves (see also *):
- Prior belief (P(H)): Initial credence in a hypothesis (e.g., “Tommy is bluffing”).
- Evidence (E): New information (e.g., a credible threat of violence, or a revealed inconsistency).
- Likelihood (P(E|H)): How likely the evidence is if the hypothesis is true.
- Posterior belief (P(H|E)): Updated belief in the hypothesis given the evidence.
In Peaky Blinders, the characters have beliefs about each other’s natures, e.g., ruthless, crazy, bluffing.
The Exchange as Bayesian Negotiation
Initial Offer – 20% (Tommy)
This reflects Tommy’s belief that Alfie will find the offer worthwhile given legal backing and mutual benefits (safe rum shipping). He assumes Alfie is rational and profit-oriented.
Alfie’s Counter – 100%
Alfie reveals a much higher demand with a threat attached (Ollie + gun). He’s signaling that he thinks Tommy has little to no leverage – a strong prior that Tommy is bluffing or weak.
Tommy’s Threat – Grenade
Tommy introduces new evidence: a possible suicide mission, planted grenade, anarchist partner. Alfie must now update his beliefs:
- What is the probability Tommy is bluffing?
- What’s the chance the grenade exists and is armed?
Ollie’s Confirmation – “He tied his lace…”
This is independent corroborating evidence – evidence of something anyway. Alfie now receives a report that raises the likelihood Tommy’s story is true (P(E|¬H) drops, P(E|H) rises). So Alfie updates his belief in Tommy’s credibility, lowering his confidence that he can push for 100%.
The offer history, which controls their priors and posteriors:
- Alfie lowers from 100% → 65% (“I’ll bet 100 to 1”)
- Tommy rejects
- Alfie considers Tommy’s past form (“he blew up his own pub”)
This shifts the prior. Now P(Tommy is reckless and serious) is higher. - Alfie: 65% → 45%
- Tommy: Counters with 30%
- Tommy adds detail: WWI tunneling expertise, same grenade kit, he blew up a mine
- Alfie checks for inconsistency (“I heard they all got buried”)
Potential Bayesian disconfirmation. Is Tommy lying? - Tommy: “Three of us dug ourselves out” → resolves inconsistency
The model regains internal coherence. Alfie’s posterior belief in the truth of the grenade story rises again. - Final offer: 35%
They settle, each having adjusted credence in the other’s threat profile and willingness to follow through.
Analysis
Beliefs are not static. Each new statement, action, or contradiction causes belief shifts. Updates are directional, not precise. No character says “I now assign 65% chance…” but, since they are rational actors, their offers directly encode these shifts in valuation. We see behaviorally expressed priors and posteriors. Alfie’s movement from 100 to 65 to 45 to 35% is not arbitrary. It reflects updates in how much control he believes he has.
Credibility is a Bayesian variable. Tommy’s past (blowing up his own pub) is treated as evidence relevant to present behavior. Social proof is given by Ollie. Ollie panics on recalling that Tommy tied his shoe. Alfie chastises Ollie for being a child in a man’s world and sends him out. But Alfie has already processed this Bayesian evidence for the grenade threat, and Tommy knows it. The 7:00 deadline adds urgency and tension to the scene. Crucially, from a Bayesian perspective, it limits the number of possible belief revisions, a typical constraint for bounded rationality.
As an initial setup, let:
- T = Tommy has rigged a grenade
- ¬T = Tommy is bluffing
- P(T) = Alfie’s prior that Tommy is serious
Let’s say initially:
P(T) = 0.15, so P(¬T) = 0.85
Alfie starts with a strong prior that Tommy’s bluffing. Most people wouldn’t blow themselves up. Tommy’s a businessman, not a suicide bomber. Alfie has armed men and controls the room.
Sequence of Evidence and Belief Updates
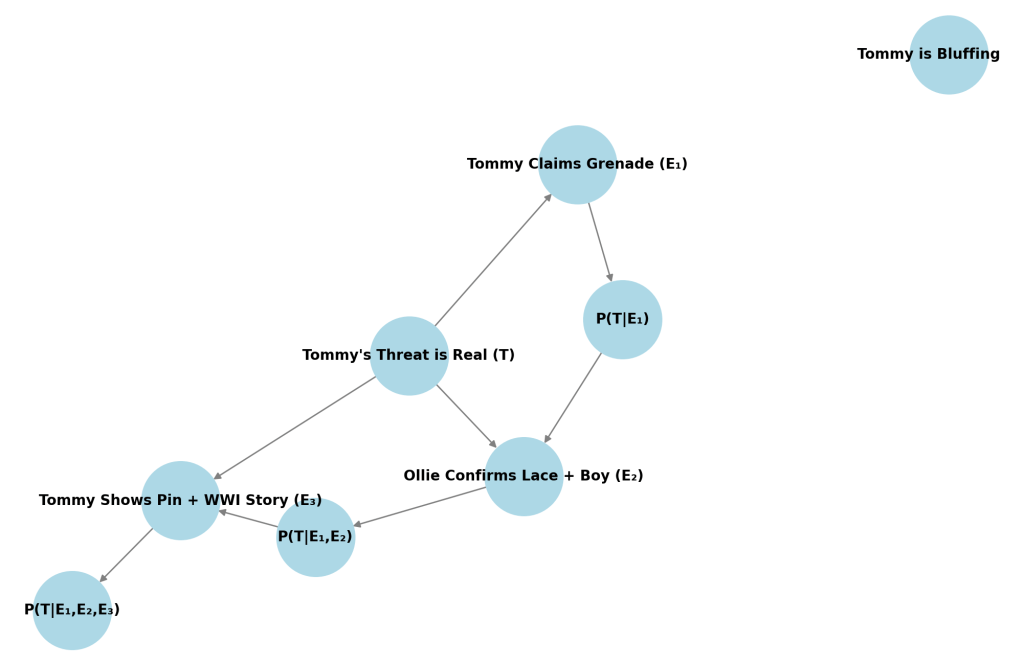
Evidence 1: Tommy’s grenade threat
E₁ = Tommy says he planted a grenade and has an assistant with a tripwire
We assign:
- P(E₁|T) = 1 (he would say so if it’s real)
- P(E₁|¬T) = 0.7 (he might bluff this anyway)
Using Bayes’ Theorem:
So now Alfie gives a 20% chance Tommy is telling the truth. Behavioral result: Alfie lowers the offer from 100% → 65%.
Evidence 2: Ollie confirms the lace-tying + nervousness
E₂ = Ollie confirms Tommy bent down and there’s a boy at the door
This is independent evidence supporting T.
- P(E₂|T) = 0.9 (if it’s true, this would happen)
- P(E₂|¬T) = 0.3 (could be coincidence)
Update:
So Alfie now gives 43% probability that the grenade is real. Behavioral result: Offer drops to 45%.
Evidence 3: Tommy shows grenade pin + WWI tunneler claim
E₃ = Tommy drops the pin and references real tunneling experience
- P(E₃|T) = 0.95 (he’d be prepared and have a story)
- P(E₃|¬T) = 0.5 (he might fake this, but riskier)
Update:
Now Alfie believes there’s nearly a 60% chance Tommy is serious. Behavioral result: Offer rises slightly to 35%, the final deal.
Simplified Utility Function
Assume Alfie’s utility is:
U(percent) = percent ⋅ V−C ⋅ P(T)
Where:
- V = Value of Tommy’s export business (let’s say 100)
- C = Cost of being blown up (e.g., 1000)
- P(T) = Updated belief Tommy is serious
So for 65%, with P(T) = 0.43:
U = 65 – 1000 ⋅ 0.43 = 65 – 430 = −365
But for 35%, with P(T) = 0.59:
U = 35 – 1000 ⋅ 0.59 = 35 – 590 = −555
Here we should note that Alfie’s utility function is not particularly sensitive to the numerical values of V and C; using C = 10,000 or 500 doesn’t change the relative outcomes much. So, why does Alfie accept the lower utility? Because risk of total loss is also a factor. If the grenade is real, pushing further ends in death and no gain. Alfie’s risk appetite is negatively skewed.
At the start of the negotiation, Alfie behaves like someone with low risk aversion by demanding 100%, assuming dominance, and later believing Tommy is bluffing. His prior is reflect extreme confidence and control. But as the conversation progresses, the downside risk becomes enormous: death, loss of business, and, likely worse, public humiliation.
The evidence increasingly supports the worst-case scenario. There’s no compensating upside for holding firm, no added reward for risking everything to get 65% instead of 35%.
This flips Alfie’s profile. He develops a sharp negative skew in risk appetite, especially under time pressure and mounting evidence. Even though 35% yields a worse expected utility than 65%, it avoids the long tail – catastrophic loss.
***
[Tommy is seated in Alfie’s office]
Alfie (to Tommy): That’ll probably be for you, won’t it?
Tommy: Hello? Arthur. You’re out.
Alfie: Right, so that’ll be your side of the street swept up, won’t it? Where’s mine? What you got for me?
Tommy: Signed by the Minister of the Empire himself. Yeah? So it is.
Tommy: This means that you can put your rum in our shipments, and no one at Poplar Docks will lift a canvas.
Alfie: You know what? I’m not even going to have my lawyer look at that.
Tommy: I know, it’s all legal.
Alfie: You know what, mate, I trust you. That’s that. Done. So, whisky… There is, uh, one thing, though, that we do need to discuss.
Tommy: What would that be?
Alfie: It says here, “20% “paid to me of your export business.”
Tommy: As we agreed on the telephone…
Alfie: No, no, no, no, no. See, I’ve had my lawyer draw this up for us, just in case. It says that, here, that 100% of your business goes to me.
Tommy: I see.
Alfie: It’s there.
Tommy: Right.
Alfie: Don’t worry about it, right, because it’s totally legal binding. All you have to do is sign the document and transfer the whole lot over to me.
Tommy: Sign just here, is it?
Alfie: Yeah.
Tommy: I see. That’s funny. That is.
Alfie: What?
Tommy: No, that’s funny. I’ll give you 100% of my business.
Alfie: Yeah.
Tommy: Why?
[Ollie appears and aims a revolver at Tommy]
Alfie: Ollie, no. No, no, no. Put that down. He understands, he understands. He’s a big boy, he knows the road. Now, look, it’s just non-fucking-negotiable. That’s all you need to know. So all you have to do is sign the fucking contract. Right there.
Tommy: just sign here?
Alfie: With your pen.
Tommy: I understand.
Alfie: Good. Get on with it.
Tommy: Well, I have an associate waiting for me at the door. I know that he looks like a choir boy, but he is actually an anarchist from Kentish Town.
Alfie: Tommy… I’m going to fucking shoot you. All right?
Tommy: Now, when I came in here, Mr. Solomons, I stopped to tie my shoelace. Isn’t that a fact? Ollie?
Tommy: I stopped to tie my shoelace. And while I was doing it, I laid a hand grenade on one of your barrels.
Tommy: Mark 15, with a wired trip. And my friend upstairs… Well, he’s like one of those anarchists that blew up Wall Street, you know? He’s a professional. And he’s in charge of the wire. If I don’t walk out that door on the stroke of 7:00, he’s going to trigger the grenade and… your very combustible rum will blow us all to hell. And I don’t care… because I’m already dead.
Ollie: He tied his lace, Alfie. And there is a kid at the door.
Tommy: From a good family, too. Ollie, it’s shocking what they become…
Alfie (to Ollie): What were you doing when this happened?
Ollie: He tied his lace, nothing else.
Alfie: Yeah, but what were you doing?
Ollie: I was marking the runners in the paper.
Alfie: What are you doing?
Tommy: Just checking the time. Carry on.
Alfie: Right, Ollie, I want you to go outside, yeah, and shoot that boy in the face – from the good family, all right?
Tommy: Anyone walks through that door except me, he blows the grenade.
Ollie: He tied his fucking lace…
Tommy: I did tie my lace.
Alfie: I bet, 100 to 1, you’re fucking lying, mate. That’s my money.
Tommy: Well, see, you’ve failed to consider the form. I did blow up me own pub… for the insurance.
Alfie: OK right… Well, considering the form, I would say 65 to 1. Very good odds. And I would be more than happy and agree if you were to sign over 65% of your business to me. Thank you.
Tommy: Sixty-five? No deal.
Alfie: Ollie, what do you say?
Ollie: Jesus Christ, Alfie. He tied his fucking lace, I saw him! He planted a grenade, I know he did. Alfie, it’s Tommy fucking Shelby…
[Alfie smacks Ollie across the face, grabs him by the collar, pulls him close and looks straight into his face.]
Alfie to Ollie: You’re behaving like a fucking child. This is a man’s world. Take your apron off, and sit in the corner like a little boy. Fuck off. Now.
Tommy: Four minutes.
Alfie: All right, four minutes. Talk to me about hand grenades.
Tommy: The chalk mark on the barrel, at knee height. It’s a Hamilton Christmas. I took out the pin and put it on the wire.
[Tommy produces a pin from his pocket and drops it on the table. Alfie inspects it.]
Alfie: Based on this… forty-five percent. [of Tommy’s business]
Tommy: Thirty.
Alfie: Oh, fuck off, Tommy. That’s far too little.
Tommy: In France, Mr. Solomons, while I was a tunneller, a clay-kicker. 179. I blew up Schwabenhöhe. Same kit I’m using today.
Alfie: It’s funny, that. I do know the 179. And I heard they all got buried.
[Alfie looks at Tommy as though he has caught him in an inconsistency]
Tommy: Three of us dug ourselves out.
Alfie: Like you’re digging yourself out now?
Tommy: Like I’m digging now.
Alfie: Fuck me. Listen, I’ll give you 35%. That’s your lot.
Tommy: Thirty-five.
[Tommy and Alfie shake hands. Tommy leaves.]
Bayes Theorem, Pearl Harbor, and the Niihau Incident
Posted by Bill Storage in Probability and Risk on July 2, 2025
The Niihau Incident of December 7–13, 1941 provides a good case study for applying Bayesian reasoning to historical events, particularly in assessing decision-making under uncertainty. Bayesian reasoning involves updating probabilities based on new evidence, using Bayes’ theorem: P(A∣B) = P(B∣A) ⋅ P(A)P(B) / P(A|B), where:
- P(E∣H) is the likelihood of observing E given H
- P(H∣E) is the posterior probability of hypothesis H given evidence E
- P(H) is the prior probability of H
- P(E) is the marginal probability of E.
Terms like P(E∣H), the probability of evidence given a hypothesis, can be confusing. Alternative phrasings may help:
- The probability of observing evidence E if hypothesis H were true
- The likelihood of E given H
- The conditional probability of E under H
These variations clarify that we’re assessing how likely the evidence is under a specific scenario, not the probability of the hypothesis itself, which is P(H∣E).
In the context of the Niihau Incident, we can use Bayesian reasoning to analyze the decisions made by the island’s residents, particularly the Native Hawaiians and the Harada family, in response to the crash-landing of Japanese pilot Shigenori Nishikaichi. Below, I’ll break down the analysis, focusing on key decisions and quantifying probabilities while acknowledging the limitations of historical data.
Context of the Niihau Incident
On December 7, 1941, after participating in the Pearl Harbor attack, Japanese pilot Shigenori Nishikaichi crash-landed his damaged A6M2 Zero aircraft on Niihau, a privately owned Hawaiian island with a population of 136, mostly Native Hawaiians. The Japanese Navy had mistakenly designated Niihau as an uninhabited island for emergency landings, expecting pilots to await rescue there. The residents, unaware of the Pearl Harbor attack, initially treated Nishikaichi as a guest but confiscating his weapons. Over the next few days, tensions escalated as Nishikaichi, with the help of Yoshio Harada and his wife Irene, attempted to destroy his plane and papers, took hostages, and engaged in violence. The incident culminated in the Kanaheles, a Hawaiian couple, overpowering and killing Nishikaichi. Yoshio Harada committing suicide.
From a Bayesian perspective, we can analyze the residents updating their beliefs as new evidence emerged.
We define two primary hypotheses regarding Nishikaichi’s intentions:
- H1: Nishikaichi is a neutral (non-threatening) lost pilot needing assistance.
- H2: Nishikaichi is an enemy combatant with hostile intentions.
The residents’ decisions reflect the updating of beliefs about (credence in) these hypotheses.
Prior Probabilities
At the outset, the residents had no knowledge of the Pearl Harbor attack. Thus, their prior probability for P(H1) (Nishikaichi is non-threatening) would likely be high, as a crash-landed pilot could reasonably be seen as a distressed individual. Conversely, P(H2) (Nishikaichi is a threat) would be low due to the lack of context about the war.
We can assign initial priors based on this context:
- P(H1) = 0.9: The residents initially assume Nishikaichi is a non-threatening guest, given their cultural emphasis on hospitality and lack of information about the attack.
- P(H2) = 0.1: The possibility of hostility exists but is less likely without evidence of war.
These priors are subjective, reflecting the residents’ initial state of knowledge, consistent with the Bayesian interpretation of probability as a degree of belief.
We identify key pieces of evidence that influenced the residents’ beliefs:
E1: Nishikaichi’s Crash-Landing and Initial Behavior
Nishikaichi crash-landed in a field near Hawila Kaleohano, who disarmed him and treated him as a guest. His initial behavior (not hostile) supports H1.
Likelihoods:
- P(E1∣H1) = 0.95: A non-threatening pilot is highly likely to crash-land and appear cooperative.
- P(E1∣H2) = 0.3: A hostile pilot could be expected to act more aggressively, though deception is possible.
Posterior Calculation:
P(H1∣E1) = [P(E1∣H1)⋅P(H1)] / [P(E1∣H1)⋅P(H1) + P(E1∣H2)⋅P(H2) ]
P(H1|E1) = 0.95⋅0.9 / [(0.95⋅0.9) + (0.3⋅0.1)] = 0.97
After the crash, the residents’ belief in H1 justifies hospitality.
E2: News of the Pearl Harbor Attack
That night, the residents learned of the Pearl Harbor attack via radio, revealing Japan’s aggression. This significantly increases the likelihood that Nishikaichi was a threat.
Likelihoods:
- P(E2∣H1) = 0.1 P(E2|H1) = 0.1 P(E2∣H1) = 0.1: A non-threatening pilot is unlikely to be associated with a surprise attack.
- P(E2∣H2) = 0.9 P(E2|H2) = 0.9 P(E2∣H2) = 0.9: A hostile pilot is highly likely to be linked to the attack.
Posterior Calculation (using updated priors from E1):
P(H1∣E2) = P(E2∣H1)⋅P(H1∣E1) / [P(E2∣H1)⋅P(H1∣E1) + P(E2∣H2)⋅P(H2∣E1)]
P(H1∣E2) = 0.1⋅0.97 / [(0.1⋅0.97) + (0.9⋅0.03)] = 0.76
P(H2∣E2) = 0.24
The news shifts the probability toward H2, prompting the residents to apprehend Nishikaichi and put him under guard with the Haradas.
E3: Nishikaichi’s Collusion with the Haradas
Nishikaichi convinced Yoshio and Irene Harada to help him escape, destroy his plane, and burn Kaleohano’s house to eliminate his papers.
Likelihoods:
- P(E3∣H1) = 0.01: A non-threatening pilot is extremely unlikely to do this.
- P(E3∣H2) = 0.95: A hostile pilot is likely to attempt to destroy evidence and escape.
Posterior Calculation (using updated priors from E2):
P(H1∣E3) = P(E3∣H1)⋅P(H1∣E2) / [P(E3∣H1)⋅P(H1∣E2) + P(E3∣H2)⋅P(H2∣E2)]
P(H1∣E3) = 0.01⋅0.759 / [(0.01⋅0.759) + (0.95⋅0.241)] = 0.032
P(H2∣E3) = 0.968
This evidence dramatically increases the probability of H2, aligning with the residents’ decision to confront Nishikaichi.
E4: Nishikaichi Takes Hostages and Engages in Violence
Nishikaichi and Harada took Ben and Ella Kanahele hostage, and Nishikaichi fired a machine gun. Hostile intent is confirmed.
Likelihoods:
- P(E4∣H1) = 0.001: A non-threatening pilot is virtually certain not to take hostages or use weapons.
- P(E4∣H2) = 0.99: A hostile pilot is extremely likely to resort to violence.
Posterior Calculation (using updated priors from E3):
P(H1∣E4) = P(E4∣H1)⋅P(H1∣E3)/ [P(E4∣H1)⋅P(H1∣E3) + P(E4∣H2)⋅P(H2∣E3)P(H1|E4)]
P(H1∣E4) = 0.001⋅0.032 / [(0.001⋅0.032)+(0.99⋅0.968)] =0.00003
P(H2∣E4) = 1.0 – P(H1∣E4) = 0.99997
At this point, the residents’ belief in H2 is near certainty, justifying the Kanaheles’ decisive action to overpower Nishikaichi.
Uncertainty Quantification
Bayesian reasoning also involves quantifying uncertainty, particularly aleatoric (inherent randomness) and epistemic (model uncertainty) components.
Aleatoric Uncertainty: The randomness in Nishikaichi’s actions (e.g., whether he would escalate to violence) was initially high due to the residents’ lack of context. As evidence accumulated, this uncertainty decreased, as seen in the near-certain posterior for H2 after E4.
Epistemic Uncertainty: The residents’ model of Nishikaichi’s intentions was initially flawed due to their isolation and lack of knowledge about the war. This uncertainty reduced as they incorporated news of Pearl Harbor and observed Nishikaichi’s actions, refining their model of his behavior.
Analysis of Decision-Making
The residents’ actions align with Bayesian updating:
Initial Hospitality (E1): High prior for H1 led to treating Nishikaichi as a guest, with precautions (disarming him) reflecting slight uncertainty.
Apprehension (E2): News of Pearl Harbor shifted probabilities toward H2, prompting guards and confinement with the Haradas.
Confrontations (E3, E4): Nishikaichi’s hostile actions (collusion, hostage-taking) pushed P(H2) to near 1, leading to the Kanaheles’ lethal response.
The Haradas’ decision to assist Nishikaichi complicates the analysis. Their priors may have been influenced by cultural or personal ties to Japan, increasing their P(H1) or introducing a separate hypothesis of loyalty to Japan. Lack of detailed psychological data makes quantifying their reasoning speculative.
Limitations and Assumptions
Subjective Priors: The assigned priors (e.g., P(H1) = 0.9) are estimates based on historical context, not precise measurements. Bayesian reasoning allows subjective priors, but different assumptions could alter results.
Likelihood Estimates: Likelihoods (e.g., P(E1∣H1) = 0.95) are informed guesses, as historical records lack data on residents’ perceptions.
Simplified Hypotheses: I used two hypotheses for simplicity. In reality, residents may have considered nuanced possibilities, e.g., Nishikaichi being coerced or acting out of desperation.
Historical Bias: may exaggerate or omit details, affecting our understanding of evidence.
Conclusion
Bayesian reasoning (Subjective Bayes) provides a structured framework to understand how Niihau’s residents updated their beliefs about Nishikaichi’s intentions. Initially, a high prior for him being non-threatening (P(H1)=0.9) was reasonable given their isolation. As evidence accumulated (news of Pearl Harbor, Nishikaichi’s collusion with the Haradas, and his violent actions) the posterior probability of hostility, P(H2) approached certainty, justifying their escalating responses. Quantifying this process highlights the rationality of their decisions under uncertainty, despite limited information. This analysis demonstrates Bayesian inference used to model historical decision-making, assuming the deciders were rational agents.
Next
The Niihau Incident influenced U.S. policy decisions regarding the internment of Japanese Americans during World War II. It heightened fears of disloyalty among Japanese Americans. Applying Bayesian reasoning to the decision to intern Japanese Americans after the Niihau Incident might provide insight on how policymakers updated their beliefs about the potential threat posed by this population based on limited evidence and priors. In a future post, I’ll use Bayes’ theorem to model this decision-making process to model the quantification of risk.
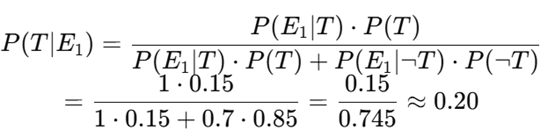
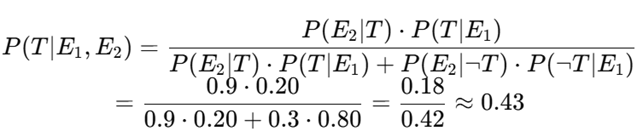
Recent Comments