The Multidisciplinarian

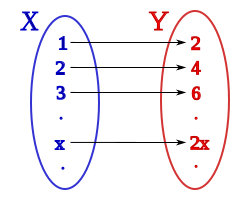
Are we too willing to accept things on authority – even in math? Proofs of the irrationality of the square root of two and of the Pythagorean theorem can be confirmed by pure deductive logic. Georg Cantor’s (d. 1918) claims on set size and countable infinity seem to me a much less secure sort of knowledge. High school algebra books (e.g., the classic Dolciani) teach 1-to-1 correspondence between the set of natural numbers and the set of even numbers as if it is a demonstrated truth. This does the student a disservice.

Following Cantor’s line of reasoning is simple enough, but it seems to treat infinity as a number, thereby passing from mathematics into philosophy. More accurately, it treats an abstract metaphysical construct as if it were math. Using Cantor’s own style of reasoning, one can just as easily show the natural and even number sets to be no non-corresponding.

Cantor demonstrated a one-to-one correspondence between natural and even numbers by showing their elements can be paired as shown below:

1 <—> 2
2 <—> 4
3 <—> 6
…
n <—> 2n

This seems a valid demonstration of one-to-one correspondence. It looks like math, but is it? I can with equal validity show the two sets (natural numbers and even numbers) to have a 2-to-1 correspondence. Consider the following pairing. Set 1 on the left is the natural numbers. Set 2 on the right is the even numbers:

1      unpaired
2 <—> 2
3      unpaired
4 <—> 4
5      unpaired
…
2n -1      unpaired
2n <—> 2n

By removing all the unpaired (odd) elements from the set 1, you can then pair each remaining member of set 1 with each element of set 2. It seems arguable that if a one to one correspondence exists between part of set 1 and all of set 2, the two whole sets cannot support a 1-to-1 correspondence. By inspection, the set of even numbers is included within the set of natural numbers and obviously not coextensive with it. Therefore Cantor’s argument, based solely on correspondence, works only by promoting one concept – the pairing of terms – while suppressing an equally obvious concept, that of inclusion. Cantor indirectly dismisses this argument against set correspondence by allowing that a set and a proper subset of it can be the same size. That allowance is not math; it is metaphysics.

Digging a bit deeper, Cantor’s use of the 1-to-1 concept (often called bijection) is heavy handed. It requires that such correspondence be established by starting with sets having their members placed in increasing order. Then it requires the first members of each set to be paired with one another, and so on. There is nothing particularly natural about this way of doing things. It got Cantor into enough of a logical corner that he had to revise the concepts of cardinality and ordinality with special, problematic definitions.

Gottlob Frege and Bertrand Russell later patched up Cantor’s definitions. The notion of equipollent sets fell out of this work, along with complications still later addressed by von Neumann and Tarski. Finally, it seems to me that Cantor implies – but fails to state outright – that the existence of a simultaneous 2-to-1 correspondence (i.e., group each n and n+1 in set 1 with each 2n in set 2 to get a 1-to-1correspondence between the two sets) does no damage to the claims that 1-to-1correspondence between the two sets makes them equal in size. In other words, Cantor helped himself to an unnaturally restrictive interpretation (i.e., a matter of language, not of math) of 1-to-1 correspondence that favored his agenda. Finally, Cantor slips a broader meaning of equality on us than the strict numerical equality the rest of math. This is a sleight of hand. Further, his usage of the term – and concept of – size requires a special definition.

Cantor’s rule set for the pairing of terms and his special definitions are perfectly valid axioms for mathematical system, but there is nothing within mathematics that justifies these axioms. Believing that the consequences of a system or theory justify its postulates is exactly the same as believing that the usefulness of Euclidean geometry justifies Euclid’s fifth postulate. Euclid knew this wasn’t so, and Proclus tells us Euclid wasn’t alone in that view.

Galileo seems to have had a more grounded sense of the infinite than did Cantor. For Galileo, the concrete concept of mathematical equality does not reconcile with the abstract concept of infinity. Galileo thought concepts like similarity, countability, size, and equality just don’t apply to the infinite. Did the development of calculus create an unwarranted acceptance of infinity as a mathematical entity? Does our understanding that things can approach infinity justify allowing infinities to be measured and compared?

Cantor’s model of infinity is interesting and useful, but it is a shame that’s it’s taught as being a matter of fact, e.g., “infinity comes in infinitely many different sizes – a fact discovered by Georg Cantor” (Science News, Jan 8, 2008).

On countable infinity we might consider WVO Quine’s position that the line between analytic (a priori) and synthetic (about the world) statements is blurry, and that no claim is immune to empirical falsification. In that light I’d argue that the above demonstration of inequality of the sets of natural and even numbers (inclusion of one within the other) trumps the demonstration of equal size by correspondence.

Mathematicians who state the equal-size concept as a fact discovered by Cantor have overstepped the boundaries of their discipline. Galileo regarded the natural-even set problem as a true paradox. I agree. Does Cantor really resolve this paradox or is he merely manipulating language?