Posts Tagged Risk management
Smart Folk Often Full of Crap, Study Finds
Posted by Bill Storage in Uncategorized on April 22, 2021
For most of us, there is a large gap between what we know and what we think we know. We hold a level of confidence about our factual knowledge and predictions that doesn’t match our abilities. Since our personal decisions are really predictions about the future based on our available present knowledge, it makes sense to work toward adjusting our confidence to match our skill.
Last year I measured the knowledge-confidence gap of 3500 participants in a trivia game with a twist. For each True/False trivia question the respondents specified their level of confidence (between 50 and 100% inclusive) with each answer. The questions, presented in banks of 10, covered many topics and ranged from easy (American stop signs have 8 sides) to expert (Stockholm is further west than Vienna).
I ran this experiment on a website and mobile app using 1500 True/False questions, about half of which belonged to specific categories including music, art, current events, World War II, sports, movies and science. Visitors could choose between the category “Various” or from a specific category. I asked for personal information such as age, gender current profession, title, and education. About 20% of site visitors gave most of that information. 30% provided their professions.
Participants were told that the point of the game was not to get the questions right but to have an appropriate level of confidence. For example, if a your average confidence value is 75%, 75% of their your answers should be correct. If your confidence and accuracy match, you are said to be calibrated. Otherwise you are either overconfident or underconfident. Overconfidence – sometime extreme – is more common, though a small percentage are significantly underconfident.
Overconfidence in group decisions is particularly troubling. Groupthink – collective overconfidence and rationalized cohesiveness – is a well known example. A more common, more subtle, and often more dangerous case exists when social effects and the perceived superiority of judgment of a single overconfident participant can leads to unconscious suppression of valid input from a majority of team members. The latter, for example, explains the Challenger launch decision for more than classic groupthink does, though groupthink is often cited as the cause.
I designed the trivia quiz system so that each group of ten questions under the Various label included one that dealt with a subject about which people are particularly passionate – environmental or social justice issues. I got this idea from Hans Rosling’s book, Factfulness. As expected, respondents were both overwhelmingly wrong and acutely overconfident about facts tied to emotional issues, e.g., net change in Amazon rainforest area in last five years.
I encouraged people to use take a few passes through the Various category before moving on to the specialty categories. Assuming that the first specialty categories that respondents chose was their favorite, I found them to be generally more overconfident about topics they presumable knew best. For example, those that first selected Music and then Art showed both higher resolution (correctness) and higher overconfidence in Music than they did in Art.
Mean overconfidence for all first-chosen specialties was 12%. Mean overconfidence for second-chosen categories was 9%. One interpretation is that people are more overconfident about that which they know best. Respondents’ overconfidence decreased progressively as they answered more questions. In that sense the system served as confidence calibration training. Relative overconfidence in the first specialty category chosen was present even when the effect of improved calibration was screened off, however.
For the first 10 questions, mean overconfidence in the Various category was 16% (16% for males, 14% for females). Mean overconfidence for the nine question in each group excepting the “passion” question was 13%.
Overconfidence seemed to be constant across professions, but increased about 1.5% with each level of college education. PhDs are 4.2% more overconfident than high school grads. I’ll leave that to sociologists of education to interpret. A notable exception was a group of analysts from a research lab who were all within a point or two of perfect calibration even on their first 10 questions. Men were slightly more overconfident than women. Underconfidence (more than 5% underconfident) was absent in men and present in 6% of the small group identifying as women (98 total).
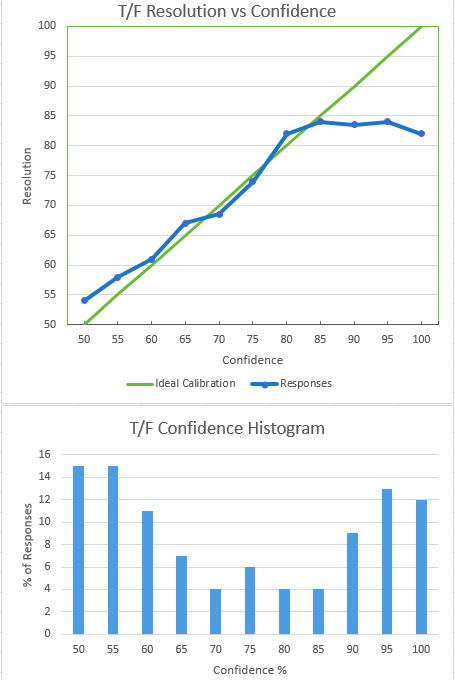
The nature of overconfidence is seen in the plot of resolution (response correctness) vs. confidence. Our confidence roughly matches our accuracy up to the point where confidence is moderately high, around 85%. After this, increased confidence occurs with no increase in accuracy. At at 100% confidence level, respondents were, on average, less correct than they were at 95% confidence. Much of that effect stemmed from the one “trick” question in each group of 10; people tend to be confident but wrong about hot topics with high media coverage.
The distribution of confidence values expressed by participants was nominally bimodal. People expressed very high or very low confidence about the accuracy of their answers. The slight bump in confidence at 75% is likely an artifact of the test methodology. The default value of the confidence slider (website user interface element) was 75%. On clicking the Submit button, users were warned if most of their responses specified the default value, but an acquiescence effect appears to have present anyway. In Superforecasters Philip Tetlock observed that many people seem to have a “three settings” (yes, no, maybe) mindset about matters of probability. That could also explain the slight peak at 75%.
I’ve been using a similar approach to confidence calibration in group decision settings for the past three decades. I learned it from a DoD publication by Sarah Lichtenstein and Baruch Fischhoff while working on the Midgetman Small Intercontinental Ballistic Missile program in the mid 1980s. Doug Hubbard teaches a similar approach in his book The Failure of Risk Management. In my experience with diverse groups contributing to risk analysis, where group decisions about likelihood of uncertain events are needed, an hour of training using similar tools yields impressive improvements in calibration as measured above.
Risk Neutrality and Corporate Risk Frameworks
Posted by Bill Storage in Uncategorized on October 27, 2020
Wikipedia describes risk-neutrality in these terms: “A risk neutral party’s decisions are not affected by the degree of uncertainty in a set of outcomes, so a risk-neutral party is indifferent between choices with equal expected payoffs even if one choice is riskier”
While a useful definition, it doesn’t really help us get to the bottom of things since we don’t all remotely agree on what “riskier” means. Sometimes, by “risk,” we mean an unwanted event: “falling asleep at the wheel is one of the biggest risks of nighttime driving.” Sometimes we equate “risk” with the probability of the unwanted event: “the risk of losing in roulette is 35 out of 36. Sometimes we mean the statistical expectation. And so on.
When the term “risk” is used in technical discussions, most people understand it to involve some combination of the likelihood (probability) and cost (loss value) of an unwanted event.
We can compare both the likelihoods and the costs of different risks, but deciding which is “riskier” using a one-dimensional range (i.e., higher vs. lower) requires a scalar calculus of risk. If risk is a combination of probability and severity of an unwanted outcome, riskier might equate to a larger value of the arithmetic product of the relevant probability (a dimensionless number between zero and one) and severity, measured in dollars.
But defining risk as such a scalar (area under the curve, therefore one dimensional) value is a big step, one that most analyses of human behavior suggests is not an accurate representation of how we perceive risk. It implies risk-neutrality.
Most people agree, as Wikipedia states, that a risk-neutral party’s decisions are not affected by the degree of uncertainty in a set of outcomes. On that view, a risk-neutral party is indifferent between all choices having equal expected payoffs.
Under this definition, if risk-neutral, you would have no basis for preferring any of the following four choices over another:
1) a 50% chance of winning $100.00
2) An unconditional award of $50.
3) A 0.01% chance of winning $500,000.00
4) A 90% chance of winning $55.56.
If risk-averse, you’d prefer choices 2 or 4. If risk-seeking, you’d prefer 1 or 3.
Now let’s imagine, instead of potential winnings, an assortment of possible unwanted events, termed hazards in engineering, for which we know, or believe we know, the probability numbers. One example would be to simply turn the above gains into losses:
1) a 50% chance of losing $100.00
2) An unconditional payment of $50.
3) A 0.01% chance of losing $500,000.00
4) A 90% chance of losing $55.56.
In this example, there are four different hazards. Many argue that rational analysis of risk entails quantification of hazard severities, independent of whether their probabilities are quantified. Above we have four risks, all having the same $50 expected value (cost), labeled 1 through 4. Whether those four risks can be considered equal depends on whether you are risk-neutral.
If forced to accept one of the four risks, a risk-neutral person would be indifferent to the choice; a risk seeker might choose risk 3, etc. Banks are often found to be risk-averse. That is, they will pay more to prevent risk 3 than to prevent risk 4, even though they have the same expected value. Viewed differently, banks often pay much more to prevent one occurrence of hazard 3 (cost = $500,000) than to prevent 9000 occurrences of hazard 4 (cost = $500,000).
Businesses compare risks to decide whether to reduce their likelihood, to buy insurance, or to take other actions. They often use a heat-map approach (sometimes called risk registers) to visualize risks. Heat maps plot probability vs severity and view any particular risk’s riskiness as the area of the rectangle formed by the axes and the point on the map representing that risk. Lines of constant risk therefore look like y = 1 / x. To be precise, they take the form of y = a/x where a represents a constant number of dollars called the expected value (or mathematical expectation or first moment) depending on area of study.
By plotting the four probability-cost vector values (coordinates) of the above four risks, we see that they all fall on the same line of constant risk. A sample curve of this form, representing a line of constant risk appears below on the left.
In my example above, the four points (50% chance of losing $100, etc.) have a large range of probabilities. Plotting these actual values on a simple grid isn’t very informative because the data points are far from the part of the plotted curve where the bend is visible (plot below on the right).
Students of high-school algebra know the fix for the problem of graphing data of this sort (monomials) is to use log paper. By plotting equations of the form described above using logarithmic scales for both axes, we get a straight line, having data points that are visually compressed, thereby taming the large range of the data, as below.
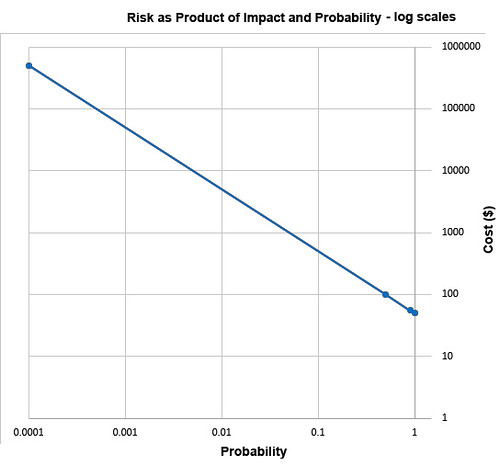
The risk frameworks used in business take a different approach. Instead of plotting actual probability values and actual costs, they plot scores, say from one ten. Their reason for doing this is more likely to convert an opinion into a numerical value than to cluster data for easy visualization. Nevertheless, plotting scores – on linear, not logarithmic, scales – inadvertently clusters data, though the data might have lost something in the translation to scores in the range of 1 to 10. In heat maps, this compression of data has the undesirable psychological effect of implying much small ranges for the relevant probability values and costs of the risks under study.
A rich example of this effect is seen in the 2002 PmBok (Project Management Body of Knowledge) published by the Project Management Institute. It assigns a score (which it curiously calls a rank) of 10 for probability values in the range of 0.5, a score of 9 for p=0.3, and a score of 8 for p=0.15. It should be obvious to most having a background in quantified risk that differentiating failure probabilities of .5, .3, and .15 is pointless and indicative of bogus precision, whether the probability is drawn from observed frequencies or from subjectivist/Bayesian-belief methods.
The methodological problem described above exists in frameworks that are implicitly risk-neutral. The real problem with the implicit risk-neutrality of risk frameworks is that very few of us – individuals or corporations – are risk-neutral. And no framework is right to tell us that we should be. Saying that it is somehow rational to be risk-neutral pushes the definition of rationality too far.
As proud king of a small distant planet of 10 million souls, you face an approaching comet that, on impact, will kill one million (10%) in your otherwise peaceful world. Your scientists and engineers rush to build a comet-killer nuclear rocket. The untested device has a 90% chance of destroying the comet but a 10% chance of exploding on launch thereby killing everyone on your planet. Do you launch the comet-killer, knowing that a possible outcome is total extinction? Or do you sit by and watch one million die from a preventable disaster? Your risk managers see two choices of equal riskiness: 100% chance of losing one million and a 10% chance of losing 10 million. The expected value is one million lives in both cases. But in that 10% chance of losing 10 million, there is no second chance. It’s an existential risk.
If these two choices seem somehow different, you are not risk-neutral. If you’re tempted to leave problems like this in the capable hands of ethicists, good for you. But unaware boards of directors have left analogous dilemmas in the incapable hands of simplistic and simple-minded risk frameworks.
The risk-neutrality embedded in risk frameworks is a subtle and pernicious case of Hume’s Guillotine – an inference from “is” to “ought” concealed within a fact-heavy argument. No amount of data, whether measured frequencies or subjective probability estimates, whether historical expenses or projected costs, even if recorded as PmBok’s scores and ranks, can justify risk-neutrality to parties who are not risk-neutral. So why is it embed it in the frameworks our leading companies pay good money for?
My Trouble with Bayes
Posted by Bill Storage in Philosophy of Science, Probability and Risk, Uncategorized on January 21, 2016
In past consulting work I’ve wrestled with subjective probability values derived from expert opinion. Subjective probability is an interpretation of probability based on a degree of belief (i.e., hypothetical willingness to bet on a position) as opposed a value derived from measured frequencies of occurrences (related posts: Belief in Probability, More Philosophy for Engineers). Subjective probability is of interest when failure data is sparse or nonexistent, as was the data on catastrophic loss of a space shuttle due to seal failure. Bayesianism is one form of inductive logic aimed at refining subjective beliefs based on Bayes Theorem and the idea of rational coherence of beliefs. A NASA handbook explains Bayesian inference as the process of obtaining a conclusion based on evidence, “Information about a hypothesis beyond the observable empirical data about that hypothesis is included in the inference.” Easier said than done, for reasons listed below.
Bayes Theorem itself is uncontroversial. It is a mathematical expression relating the probability of A given that B is true to the probability of B given that A is true and the individual probabilities of A and B:
P(A|B) = P(B|A) x P(A) / P(B)
If we’re trying to confirm a hypothesis (H) based on evidence (E), we can substitute H and E for A and B:
P(H|E) = P(E|H) x P(H) / P(E)
To be rationally coherent, you’re not allowed to believe the probability of heads to be .6 while believing the probability of tails to be .5; the sum of chances of all possible outcomes must sum to exactly one. Further, for Bayesians, the logical coherence just mentioned (i.e., avoidance of Dutch book arguments) must hold across time (synchronic coherence) such that once new evidence E on a hypothesis H is found, your believed probability for H given E should equal your prior conditional probability for H given E.
Plenty of good sources explain Bayesian epistemology and practice far better than I could do here. Bayesianism is controversial in science and engineering circles, for some good reasons. Bayesianism’s critics refer to it as a religion. This is unfair. Bayesianism is, however, like most religions, a belief system. My concern for this post is the problems with Bayesianism that I personally encounter in risk analyses. Adherents might rightly claim that problems I encounter with Bayes stem from poor implementation rather than from flaws in the underlying program. Good horse, bad jockey? Perhaps.
Problem 1. Subjectively objective
Bayesianism is an interesting mix of subjectivity and objectivity. It imposes no constraints on the subject of belief and very few constraints on the prior probability values. Hypothesis confirmation, for a Bayesian, is inherently quantitative, but initial hypotheses probabilities and the evaluation of evidence is purely subjective. For Bayesians, evidence E confirms or disconfirms hypothesis H only after we establish how probable H was in the first place. That is, we start with a prior probability for H. After the evidence, confirmation has occurred if the probability of H given E is higher than the prior probability of H, i.e., P(H|E) > P(H). Conversely, E disconfirms H when P(H|E) < P(H). These equations and their math leave business executives impressed with the rigor of objective calculation while directing their attention away from the subjectivity of both the hypothesis and its initial prior.
2. Rational formulation of the prior
Problem 2 follows from the above. Paranoid, crackpot hypotheses can still maintain perfect probabilistic coherence. Excluding crackpots, rational thinkers – more accurately, those with whom we agree – still may have an extremely difficult time distilling their beliefs, observations and observed facts of the world into a prior.
3. Conditionalization and old evidence
This is on everyone’s short list of problems with Bayes. In the simplest interpretation of Bayes, old evidence has zero confirming power. If evidence E was on the books long ago and it suddenly comes to light that H entails E, no change in the value of H follows. This seems odd – to most outsiders anyway. This problem gives rise to the game where we are expected to pretend we never knew about E and then judge how surprising (confirming) E would have been to H had we not know about it. As with the general matter of maintaining logical coherence required for the Bayesian program, it is extremely difficult to detach your knowledge of E from the rest of your knowing about the world. In engineering problem solving, discovering that H implies E is very common.
4. Equating increased probability with hypothesis confirmation.
My having once met Hillary Clinton arguably increases the probability that I may someday be her running mate; but few would agree that it is confirming evidence that I will do so. See Hempel’s raven paradox.
5. Stubborn stains in the priors
Bayesians, often citing success in the business of establishing and adjusting insurance premiums, report that the initial subjectivity (discussed in 1, above) fades away as evidence accumulates. They call this washing-out of priors. The frequentist might respond that with sufficient evidence your belief becomes irrelevant. With historical data (i.e., abundant evidence) they can calculate P of an unwanted event in a frequentist way: P = 1-e to the power -RT, roughly, P=RT for small products of exposure time T and failure rate R (exponential distribution). When our ability to find new evidence is limited, i.e., for modeling unprecedented failures, the prior does not get washed out.
6. The catch-all hypothesis
The denominator of Bayes Theorem, P(E), in practice, must be calculated as the sum of the probability of the evidence given the hypothesis plus the probability of the evidence given not the hypothesis:
P(E) = [P(E|H) x p(H)] + [P(E|~H) x P(~H)]
But ~H (“not H”) is not itself a valid hypothesis. It is a family of hypotheses likely containing what Donald Rumsfeld famously called unknown unknowns. Thus calculating the denominator P(E) forces you to pretend you’ve considered all contributors to ~H. So Bayesians can be lured into a state of false choice. The famous example of such a false choice in the history of science is Newton’s particle theory of light vs. Huygens’ wave theory of light. Hint: they are both wrong.
7. Deference to the loudmouth
This problem is related to no. 1 above, but has a much more corporate, organizational component. It can’t be blamed on Bayesianism but nevertheless plagues Bayesian implementations within teams. In the group formulation of any subjective probability, normal corporate dynamics govern the outcome. The most senior or deepest-voiced actor in the room drives all assignments of subjective probability. Social influence rules and the wisdom of the crowd succumbs to a consensus building exercise, precisely where consensus is unwanted. Seidenfeld, Kadane and Schervish begin “On the Shared Preferences of Two Bayesian Decision Makers” with the scholarly observation that an outstanding challenge for Bayesian decision theory is to extend its norms of rationality from individuals to groups. Their paper might have been illustrated with the famous photo of the exploding Challenger space shuttle. Bayesianism’s tolerance of subjective probabilities combined with organizational dynamics and the shyness of engineers can be a recipe for disaster of the Challenger sort.
All opinions welcome.
The Onagawa Reactor Non-Meltdown
Posted by Bill Storage in Risk Management on April 19, 2014
On March 11, 2011, the strongest earthquake in Japanese recorded history hit Tohuku, leaving about 15,000 dead. The closest nuclear reactor to the quake’s epicenter was the Onagawa Nuclear Power Station operated by Tohoku Electric Power Company. As a result of the earthquake and subsequent tsunami that destroyed the town of Onagawa, the Onagawa nuclear facility remained intact and shut itself down safely, without incident. The Onagawa nuclear facility was the vicinity’s only safe evacuation destination. Residents of Onagawa left homeless by the natural disasters sought refuge in the facility, where its workers provided food.
The more famous Fukushima nuclear facility was about twice as far from the earthquake’s epicenter. The tsunami at Fukushima was slightly less severe. Fukushimia experienced three core meltdowns, resulting in evacuation of 300,000 people. The findings of the Fukushima Nuclear Accident Independent Investigation Commission have been widely published. They conclude that Fukushima failed to meet the most basic safety requirements, had conducted no valid probabilistic risk assessment, had no provisions for containing damage, and that its regulators operated in a network of corruption, collusion, and nepotism. Kiyoshi Kurokawa, Chairman of the commission stated:
THE EARTHQUAKE AND TSUNAMI of March 11, 2011 were natural disasters of a magnitude that shocked the entire world. Although triggered by these cataclysmic events, the subsequent accident at the Fukushima Daiichi Nuclear Power Plant cannot be regarded as a natural disaster. It was a profoundly manmade disaster – that could and should have been foreseen and prevented.
Only by grasping [the mindset of Japanese bureaucracy] can one understand how Japan’s nuclear industry managed to avoid absorbing the critical lessons learned from Three Mile Island and Chernobyl. It was this mindset that led to the disaster at the Fukushima Daiichi Nuclear Plant.
The consequences of negligence at Fukushima stand out as catastrophic, but the mindset that supported it can be found across Japan.
Despite these findings, the world’s response to Fukushima has been much more focused on opposition to nuclear power than on opposition to corrupt regulatory government bodies and the cultures that foster them.
Two scholars from USC, Airi Ryu and Najmedin Meshkati, recently published “Why You Haven’t Heard About Onagawa Nuclear Power Station after the Earthquake and Tsunami of March 11, 2011,” their examination of the contrasting safety mindsets of TEPCO, the firm operating the Fukushima nuclear plant, and Tohoku Electric Power, the firm operating Onagawa.
Ryu and Meshkati reported vast differences in personal accountability, leadership values, work environments, and approaches to decision-making. Interestingly, they found even Tohuko Electric to be weak in setting up an environment where concerns could be raised and where an attitude of questioning authority was encouraged. Nevertheless, TEPCO was far inferior to Tohoku Electric in all other safety culture traits.
Their report is worth a read for anyone interested in the value of creating a culture of risk management and the need for regulatory bodies to develop non-adversarial relationships with the industries they oversee, something I discussed in a recent post on risk management.
A New Era of Risk Management?
Posted by Bill Storage in Probability and Risk, Risk Management on February 9, 2014
The quality of risk management has mostly fallen for the past few decades. There are signs of change for the better.
Risk management is a broad field; many kinds of risk must be managed. Risk is usually defined in terms of probability and cost of a potential loss. Risk management, then, is the identification, assessment and prioritization of risks and the application of resources to reduce the probability and/or cost of the loss.
The earliest and most accessible example of risk management is insurance, first documented in about 1770 BC in the Code of Hammurabi (e.g., rules 23, 24, and 48). The Code addresses both risk mitigation, through threats and penalties, and minimizing loss to victims, through risk pooling and insurance payouts.
Insurance was the first example of risk management getting serious about risk assessment. Both the frequentist and quantified subjective risk measurement approaches (see recent posts on belief in probability) emerged from actuarial science developed by the insurance industry.
Risk assessment, through its close relatives, decision analysis and operations research, got another boost from World War II. Big names like Alan Turing, John Von Neumann, Ian Fleming (later James Bond author) and teams at MIT, Columbia University and Bletchley Park put quantitative risk analyses of several flavors on the map.
Today, “risk management” applies to security guard services, portfolio management, terrorism and more. Oddly, much of what is called risk management involves no risk assessment at all, and is therefore inconsistent with the above definition of risk management, paraphrased from Wikipedia.
Most risk assessment involves quantification of some sort. Actuarial science and the probabilistic risk analyses used in aircraft design are probably the “hardest” of the hard risk measurement approaches, Here, “hard” means the numbers used in the analyses come from measurements of real world values like auto accidents, lightning strikes, cancer rates, and the historical failure rates of computer chips, valves and motors. “Softer” analyses, still mathematically rigorous, involve quantified subjective judgments in tools like Monte Carlo analyses and Bayesian belief networks. As the code breakers and submarine hunters of WWII found, trained experts using calibrated expert opinions can surprise everyone, even themselves.
A much softer, yet still quantified (barely), approach to risk management using expert opinion is the risk matrix familiar to most people: on a scale of 1 to 4, rate the following risks…, etc. It’s been shown to be truly worse than useless in many cases, for a variety of reasons by many researchers. Yet it remains the core of risk analysis in many areas of business and government, across many types of risk (reputation, credit, project, financial and safety). Finally, some of what is called risk management involves no quantification, ordering, or classifying. Call it expert intuition or qualitative audit.
These soft categories of risk management most arouse the ire of independent and small-firm risk analysts. Common criticisms by these analysts include:
1. “Risk management” has become jargonized and often involves no real risk analysis.
2. Quantification of risk in some spheres is plagued by garbage-in-garbage-out. Frequency-based models are taken as gospel, and believed merely because they look scientific (e.g., Fukushima).
3. Quantified/frequentist risk analyses are not used in cases where historical data and a sound basis for them actually exists (e.g., pharmaceutical manufacture).
4. Big consultancies used their existing relationships to sell unsound (fluff) risk methods, squeezing out analysts with sound methods (accused of Arthur Anderson, McKinsey, Bain, KPMG).
5. Quantitative risk analyses of subjective type commonly don’t involve training or calibration of those giving expert opinions, thereby resulting in incoherent (in the Bayesian sense) belief systems.
6. Groupthink and bad management override rational input into risk assessment (subprime mortgage, space shuttle Challenger).
7. Risk management is equated with regulatory compliance (banking operations, hospital medicine, pharmaceuticals, side-effect of Sarbanes-Oxley).
8. Some professionals refuse to accept any formal approach to risk management (medical practitioners and hospitals).
While these criticisms may involve some degree of sour grapes, they have considerable merit in my view, and partially explain the decline in quality of risk management. I’ve worked in risk analysis involving uranium processing, nuclear weapons handling, commercial and military aviation, pharmaceutical manufacture, closed-circuit scuba design, and mountaineering. If the above complaints are valid in these circles – and they are – it’s easy to believe they plague areas where softer risk methods reign.
Several books and scores of papers specifically address the problems of simple risk-score matrices, often dressed up in fancy clothes to look rigorous. The approach has been shown to have dangerous flaws by many analysts and scholars, e.g., Tony Cox, Sam Savage, Douglas Hubbard, and Laura-Diana Radu. Cox shows examples where risk matrices assign higher qualitative ratings to quantitatively smaller risks. He shows that risks with negatively correlated frequencies and severities can result in risk-matrix decisions that are worse than random decisions. Also, such methods are obviously very prone to range compression errors. Most interestingly, in my experience, the stratification (highly likely, somewhat likely, moderately likely, etc.) inherent in risk matrices assume common interpretation of terms across a group. Many tests (e.g., Kahneman & Tversky and Budescu, Broomell, Por) show that large differences in the way people understand such phrases dramatically affect their judgments of risk. Thus risk matrices create the illusion of communication and agreement where neither are present.
Nevertheless, the risk matrix has been institutionalized. It is embraced by government (MIL-STD-882), standards bodies (ISO 31000), and professional societies (Project Management Institute (PMI), ISACA/COBIT). Hubbard’s opponents argue that if risk matrices are so bad, why do so many people use them – an odd argument, to say the least. ISO 31000, in my view, isn’t a complete write-off. In places, it rationally addresses risk as something that can be managed through reduction of likelihood, reduction of consequences, risk sharing, and risk transfer. But elsewhere it redefines risk as mere uncertainty, thereby reintroducing the positive/negative risk mess created by economist Frank Knight a century ago. Worse, from my perspective, like the guidelines of PMI and ISACA, it gives credence to structure in the guise of knowledge and to process posing as strategy. In short, it sets up a lot of wickets which, once navigated, give a sense that risk has been managed when in fact it may have been merely discussed.
A small benefit of the subprime mortgage meltdown of 2008 was that it became obvious that the financial risk management revolution of the 1990s was a farce, exposing a need for deep structural changes. I don’t follow financial risk analysis closely enough to know whether that’s happened. But the negative example made public by the housing collapse has created enough anxiety in other disciplines to cause some welcome reappraisals.
There is surprising and welcome activity in nuclear energy. Several organizations involved in nuclear power generation have acknowledged that we’ve lost competency in this area, and have recently identified paths to address the challenges. The Nuclear Energy Institute recently noted that while Fukushima is seen as evidence that probabilistic risk analysis (PRA) doesn’t work, if Japan had actually embraced PRA, the high risk of tsunami-induced disaster would have been immediately apparent. Late last year the Nuclear Energy Institute submitted two drafts to the U.S. Nuclear Regulatory Commission addressing lost ground in PRA and identifying a substantive path forward: Reclaiming the Promise of Risk-Informed Decision-Making and Restoring Risk-Informed Regulation. These documents acknowledge that the promise of PRA has been stunted by distrust of the method, focus on compliance instead of science, external audits by unqualified teams, and the above-mentioned Fukushima fallacy.
Likewise, the FDA, often criticized for over-regulating and over-reach – confusing efficacy with safety – has shown improvement in recent years. It has revised its decades-old process validation guidance to focus more on verification, scientific evidence and risk analysis tools rather than validation and documentation. The FDA’s ICH Q9 (Quality Risk Management) guidelines discuss risk, risk analysis and risk management in terms familiar to practitioners of “hard” risk analysis, even covering fault tree analysis (the “hardest” form of PRA) in some detail. The ASTM E2500 standard moves these concepts further forward. Similarly, the FDA’s recent guidelines on mobile health devices seem to accept that the FDA’s reach should not exceed its grasp in the domain of smart phones loaded with health apps. Reading between the lines, I take it that after years of fostering the notion that risk management equals regulatory compliance, the FDA realized that it must push drug safety far down into the ranks of the drug makers in the same way the FAA did with aircraft makers (with obvious success) in the late 1960s. Fostering a culture of safety rather than one of compliance distributes the work of providing safety and reduces the need for regulators to anticipate every possible failure of every step of every process in every drug firm.
This is real progress. There may yet be hope for financial risk management.
Belief in Probability – Part 2
Posted by Bill Storage in Probability and Risk, Systems Engineering on December 19, 2013
Last time I started with my friend Willie’s bold claim that he doesn’t believe in probability; then I gave a short history of probability. I observed that defining probability is a controversial matter, split between objective and subjective interpretations. About the only thing these interpretations agree on is that probability values range from zero to one, where P = 1 means certainty. When you learn probability and statistics in school, you are getting the frequentist interpretation, which is considered objective. Frequentism relies on directly equating observed frequencies with probabilities. In this model, the probability of an event exactly equals the limit of the relative frequency of that outcome in an infinitely large number of trials.
The problem with this interpretation in practice – in medicine, engineering, and gambling machines – isn’t merely the impossibility of an infinite number of trials. A few million trials might be enough. Running trials works for dice but not for earthquakes and space shuttles. It also has problems with things like cancer, where plenty of frequency data exists. Frequentism requires placing an individual specimen into a relevant population or reference class. Doing this is easy for dice, harder for humans. A study says that as a white males of my age I face a 7% probability of having a stroke in the next 10 years. That’s based on my membership in the reference class of white males. If I restrict that set to white men who don’t smoke, it drops to 4%. If I account for good systolic blood pressure, no family history of atrial fibrillation or ventricular hypertrophy, it drops another percent or so.
Ultimately, if I limit my population to a set of one (just me) and apply the belief that every effect has a cause (i.e., some real-world chunk of blockage causes an artery to rupture), you can conclude that my probability of having a stroke can only be one of two values – zero or one.
Frequentism, as seen by its opponents, too closely ties probabilities to observed frequencies. They note that the limit-of-relative-frequency concept relies on induction, which might mean it’s not so objective after all. Further, those frequencies are unknowable in many real-world cases. Still further, finding an individual’s correct reference class is messy, possibly downright subjective. Finally, no frequency data exists for earthquakes that haven’t happened yet. All that seems to do some real damage to frequentism’s utility score.
The subjective interpretations of probability propose fixes to some of frequentism’s problems. The most common subjective interpretation is Bayesianism, which itself comes in several flavors. All subjective interpretations see probability as a degree of belief in a specific outcome, as held by a rational person. Think of it as a fair bet with odds. The odds you’re willing to accept for a bet on your race horse exactly equals your degree of belief in that horse’s ability to win. If your filly were in the same race an infinite number of times, you’d expect to break even, based on those odds, whether you bet on her or against her.
Subjective interpretations rely on logical coherence and belief. The core of Bayesianism, for example, is that beliefs must 1) originate with a numerical probability estimate, 2) adhere to the rules of probability calculation, and 3) follow an exact rule for updating belief estimates based on new evidence. The second rule deals with the common core of probability math used in all interpretations. These include things like how to add and multiply probabilities and Bayes theorem, not to be confused with Bayesianism, the belief system. Bayes theorem is an uncontroversial equation relating the probability of A given B to the probability of A and the probability of B. The third rule of Bayesianism is similarly computational, addressing how belief is updated after new evidence. The details aren’t needed here. Note that while Bayesianism is generally considered subjective, it is still computationally exacting.
The obvious problem with all subjective interpretations, particularly as applied to engineering problems, is that they rely, at least initially, on expert opinion. Life and death rides on the choice of experts and the value of their opinions. As Richard Feynman noted in his minority report on the Challenger, official rank plays too large a part in the choice of experts, and the higher (and less technical) the rank, the more optimistic the probability estimates.
The engineering risk analysis technique most consistent with the frequentist (objective) interpretation of probability is fault tree analysis. Other risk analysis techniques, some embodied in mature software products, are based on Bayesian (subjective) philosophy.
When Willie said he didn’t believe in probability, he may have meant several things. I’ll try to track him down and ask him, but I doubt the incident stuck in his mind as it did mine. If he meant that he doesn’t believe that probability was useful in system design, he had a rational belief; but I disagree with it. I doubt he meant that though.
Willie may have been leaning toward the ties between probability and redundancy in system design. Probability is the calculus by which redundancy is allocated to redundant systems. Willie may think that redundancy doesn’t yield the expected increase in safety because having more equipment means more things than can fail. This argument fails to face that, ideally speaking, a redundant path does double the chance having a component failure, but squares the probability of system failure. That’s a good thing, since squaring a number less than one makes it smaller. In other words, the benefit in reducing the chance of system failure vastly exceeds the deficit of having more components to repair. If that was his point, I disagree in principle, but accept that redundancy is no excuse for lack of component design excellence.
He may also think system designers can be overly confident of the exponential increase in modeled probability of system reliability that stems from redundancy. That increase in reliability is only valid if the redundancy creates no common mode failures and no latent (undetected for unknown time intervals) failures of redundant paths that aren’t currently operating. If that’s his point, then we agree completely. This is an area where pairing the experience and design expertise of someone like Willie with rigorous risk analysis using fault trees yields great systems.
Unlike Willie, Challenger-era NASA gave no official statement on its belief in probability. Feynman’s report points to NASA’s use of numeric probabilities for specific component failure modes. The Rogers Commission report says that NASA management talked about degrees of probability. From this we might guess that NASA believed in probability and its use in measuring risk. On the other hand, the Rogers Commission report also gives examples of NASA’s disbelief in probability’s usefulness. For example, the report’s Technical Management section states that, “NASA has rejected the use of probability on the basis that such techniques are insufficient to assure that adequate safety margins can be applied to protect the lives of the crew.”
Regardless of what NASA’s beliefs about porbability, it’s clear that NASA didn’t use fault tree analysis for the space shuttle program prior to the Challenger disaster. Nor did it use Bayesian inference methods, any hybrid probability model, or any consideration of probability beyond opinions about failures of critical items. Feynman was livid about this. A Bayesian (subjective, but computational) approach would have at least forced NASA to make it subjective judgments explicit and would have produced a rational model of its judgments. Post-Challenger Bayesian analyses, including one by NASA, varied widely, but all indicated unacceptable risk. NASA has since adopted risk management approaches more consistent with those used in commercial and military aircraft design.
An obvious question arises when you think about using a frequentist model on nearly one-of-a-kind vehicles. How accurate can any frequency data be for something as infrequent as a shuttle flight? Accurate enough, in my view. If you see the shuttle as monolithic and indivisible, the data is too sparse; but not if you view it as a system of components, most of which, like o-ring seals, have close analogs in common use, with known failure rates.
The FAA mandated probabilistic risk analyses of the frequentist variety (effectively mandating fault trees) in 1968. Since then flying has become safe, by any measure. In no other endeavor has mankind made such an inherently dangerous activity so safe. Aviation safety progressed through many innovations, redundant systems being high on the list. Probability is the means by which you allocate redundancy. You can’t get great aircraft systems without designers like Willie. Nor can you get them without probability. Believe it or not.
Belief in Probability – Part 1
Posted by Bill Storage in Aerospace, Probability and Risk, Risk Management, Systems Engineering on December 18, 2013
Years ago in a meeting on design of a complex, redundant system for a commercial jet, I referred to probabilities of various component failures. In front of this group of seasoned engineers, a highly respected, senior member of the team interjected, “I don’t believe in probability.” His proclamation stopped me cold. My first thought was what kind a backward brute would say something like that, especially in the context of aircraft design. But Willie was no brute. In fact he is a legend in electro-hydro-mechanical system design circles; and he deserves that status. For decades, millions of fearless fliers have touched down on the runway, unaware that Willie’s expertise played a large part in their safe arrival. So what can we make of Willie’s stated disbelief in probability?
Friends and I have been discussing risk science a lot lately – diverse aspects of it including the Challenger disaster, pharmaceutical manufacture in China, and black swans in financial markets. I want to write a few posts on risk science, as a personal log, and for whomever else might be interested. Risk science relies on several different understandings of risk, which in turn rely on the concept of probability. So before getting to risk, I’m going to jot down some thoughts on probability. These thoughts involve no computation or equations, but they do shed some light on Willie’s mindset. First a bit of background.
Oddly, the meaning of the word probability involves philosophy much more than it does math, so Willie’s use of belief might be justified. People mean very different things when they say probability. The chance of rolling a 7 is conceptually very different from the chance of an earthquake in Missouri this year. Probability is hard to define accurately. A look at its history shows why.
Mathematical theories of probability only first appeared in the late 17th century. This is puzzling, since gambling had existed for thousands of years. Gambling was enough of a problem in the ancient world that the Egyptian pharaohs, Roman emperors and Achaemenid satraps outlawed it. Such legislation had little effect on the urge to deal the cards or roll the dice. Enforcement was sporadic and halfhearted. Yet gamblers failed to develop probability theories. Historian Ian Hacking (The Emergence of Probability) observes, “Someone with only the most modest knowledge of probability mathematics could have won himself the whole of Gaul in a week.”
Why so much interest with so little understanding? In European and middle eastern history, it seems that neither Platonism (determinism derived from ideal forms) nor the Judeo/Christian/Islamic traditions (determinism through God’s will) had much sympathy for knowledge of chance. Chance was something to which knowledge could not apply. Chance meant uncertainty, and uncertainty was the absence of knowledge. Knowledge of chance didn’t seem to make sense. Plus, chance was the tool of immoral and dishonest gamblers.
The term probability is tied to the modern understanding of evidence. In medieval times, and well into the renaissance, probability literally referred to the level of authority – typically tied to the nobility – of a witness in a court case. A probable opinion was one given by a reputable witness. So a testimony could be highly probable but very incorrect, even false.
Through empiricism, central to the scientific method, the notion of diagnosis (inference of a condition from key indicators) emerged in the 17th century. Diagnosis allowed nature to be the reputable authority, rather than a person of status. For example, the symptom of skin spots could testify, with various degrees of probability, that measles had caused it. This goes back to the notion of induction and inference from the best explanation of evidence, which I discussed in past posts. Pascal, Fermat and Huygens brought probability into the respectable world of science.
But outside of science, probability and statistics still remained second class citizens right up to the 20th century. You used these tools when you didn’t have an exact set of accurate facts. Recognition of the predictive value of probability and statistics finally emerged when governments realized that death records had uses beyond preserving history, and when insurance companies figured out how to price premiums competitively.
Also around the turn of the 20th century, it became clear that in many realms – thermodynamics and quantum mechanics for example – probability would take center stage against determinism. Scientists began to see that some – perhaps most – aspects of reality were fundamentally probabilistic in nature, not deterministic. This was a tough pill for many to swallow, even Albert Einstein. Einstein famously argued with Niels Bohr, saying, “God does not play dice.” Einstein believed that some hidden variable would eventually emerge to explain why one of two identical atoms would decay while the other did not. A century later, Bohr is still winning that argument.
What we mean when we say probability today may seem uncontroversial – until you stake lives on it. Then it gets weird, and definitions become important. Defining probability is a wickedly contentious matter, because wildly conflicting conceptions of probability exist. They can be roughly divided into the objective and subjective interpretations. In the next post I’ll focus on the frequentist interpretation, which is objective, and the subjectivist interpretations as a group. I’ll look at the impact of accepting – or believing in – each of these on the design of things like airliners and space shuttles from the perspectives of Willie, Richard Feynman, and NASA. Then I’ll defend my own views on when and where to hold various beliefs about probability.
Is Fault Tree Analysis Deductive?
Posted by Bill Storage in Engineering, Probability and Risk, Risk Management on December 2, 2013
An odd myth persists in systems engineering and risk analysis circles. Fault tree analysis (FTA), and sometimes fault trees themselves, are said to be deductive. FMEAs are called inductive. How can this be?
By fault trees I mean Boolean logic modeling of unwanted system states by logical decomposition of equipment fault states into combinations of failure states of more basic components. You can read more on fault tree analysis and its deductive nature at Wikipedia. By FMEA (Failure Mode & Effects Analysis) I mean recording all the things that can go wrong with the components of a system. Writers who find fault trees deductive also find FMEAs, their complement, to be inductive. I’ll argue here that building fault trees is not a deductive process, and that there is possible harm in saying so. Secondarily, I’ll offer that while FMEA creation involves inductive reasoning, the point carries little weight, since the rest of engineering is inductive reasoning too.
Word meanings can vary with context; but use of the term deductive is consistent across math, science, law, and philosophy. Deduction is the process of drawing a logically certain conclusion about a particular instance from a rule or premise about the general. Assuming all men are mortal, if Socrates is a man, then he is mortal. This is true regardless of the meaning of the word mortal. It’s truth is certain, even if Socrates never existed, and even if you take mortal to mean living forever.
Example from a software development website:
FMECA is an inductive analysis of system failure, starting with the presumed failure of a component and analyzing its effect on system stability: “What will happen if valve A sticks open?” In contrast, FTA is a deductive analysis, starting with potential or actual failures and deducing what might have caused them: “What could cause a deadlock in the application?”
The well-intended writer says we deduce the causes of the effects in question. Deduction is not up to that task. When we infer causes from observed effects, we are using induction, not deduction.
How did the odd claims that fault trees and FTAs are deductive arise? It might trace to William Vesely, NASA’s original fault tree proponent. Vesely sometimes used the term deductive in his introductions to fault trees. If he meant that the process of reducing fault trees into cut sets (sets of basic events or initiators) is deductive, he was obviously correct. But calculation isn’t the critical aspect of fault trees; constructing them is where the effort and need for diligence lie. Fault tree software does the math. If Vesely saw the critical process of constructing fault trees and supplying them with numerical data (often arduous, regardless of software) as deductive – which I doubt – he was certainly wrong.
Inductive reasoning, as used in science, logic and philosophy, means inferring general rules or laws from observations of particular instances. The special use of the term math induction actually refers to deduction, as mathematicians are well aware. Math induction is deductive reasoning with a confusing title. Induction in science and engineering stems from our need to predict future events. We form theories about how things will behave in the future based on observations of how similar things behaved in the past. As I discussed regarding Bacon vs. Descartes, science is forced into the realm of induction because deduction never makes contact with the physical world – it lives in the mind.
Inductive reasoning is exactly what goes on when you construct a fault tree. You are making inferences about future conditions based on modeling and historical data – a purely inductive process. The fact that you use math to solve fault trees does not make fault trees any more deductive than the presence of math in lab experiments makes empirical science deductive.
Does this matter?
It’s easy enough to fix this technical point in descriptions fault tree analysis. We should do so, if merely to avoid confusing students. But more importantly, quantitative risk analysis – including FTA – has its enemies. They range from several top consultancies selling subjective, risk-score matrix methodologies dressed up in fancy clothes (see Tony Cox’s SIRA presentation on this topic) to some of NASA’s top management – those flogged by Richard Feynman in his minority report on the Challenger disaster. The various criticisms of fault tree analysis say it is too analytical and correlates poorly with the real world. Sound familiar? It echoes a feud between the heirs of Bacon (induction) and the heirs of Descartes (deduction). Some of fault trees’ foes find them overly deductive. They then imply that errors found in past quantitative analyses impugn objectivity itself, preferring subjective analyses based on expert opinion. This curious conclusion would not follow, even if fault tree analyses were deductive, which they are not.
.
——————————————
Science is the belief in the ignorance of experts. – Richard Feynman
.
.
The Multidisciplinarian 
Recent Comments