Extraordinary Popular Miscarriages of Science, part 4 – Marxism
Posted by Bill Storage in History of Science on February 24, 2024
Marxists are ignorant. In a very literal sense. They are capable of willfully ignoring the universe of evidence showing the fundamentals of Marxian thought to have been disproved before Marx’s ink dried. Maybe some of them are just childish or stupid. They can be excused. But most Marxists are intelligent adults who have made a bad faith decision to pretend that their theory is not disproved by every semiconductor in their cars and mobile phones, and every LED light bulb in existence. Every Marxist book denouncing private property is copyrighted. They want us to free ourselves of the restraints that made freedom possible.

Marx was a spoiled lout who never worked an honest day in his life, rarely repaid his unending loans, disparaged his creditors, blamed his infant son’s death on capitalism while he remained drunk and lived in squalor, abused his maid – whom he never paid a cent – and described Ferdinand Lassalle as “the Jewish Nigger Lassalle.” In his essay “On the Jewish Question,” Marx wrote that “The social emancipation of the Jew is the emancipation of society from Jewishness.” There’s lots more where those come from.
Marx wanted “… not to improve the existing society but to found a new one.” His writings for the Central Committee of the Communist League was devoured and put into practice by Lenin, resulting in genocide. His thought fueled totalitarian despots like Stalin, Mao, and Pol Pot, and the attempts to implement his poorly expressed ideas caused mass starvation, cultural stagnation, and tens of millions of deaths. Yet he probably has more influence on academic thought than Galileo, Newton, and Einstein. Pillars of the academic left are quick to point out that Marx would be horrified to find his words being used to defend the use of state power against individuals. Yet those words were quoted liberally by Lenin in defense of autocratic power and murder. Those self-important academic indoctrinators somehow imagine that there could be a different interpretation of Marx by the average power-hungry psychopath.
Marx was a miserable person, in every sense. His Doctrine of Misery is endlessly analyzed by intellectuals, though they cannot agree on what it is exactly. All boats simply cannot rise under Marxism. It’s a zero sum game. Where Marx occasionally leans toward admitting that all boats could in theory rise, his complaint reduces to envy. Better for all to starve than for some to have burgers while others eat fillet mignon.
“Thus although the enjoyments of the workers have risen, the social satisfaction that they give has fallen in comparison with the increased enjoyments of the capitalist, which are inaccessible to the worker.”
Marx’s poetry sheds light on his self-image. In one he penned, “with disdain I will throw my gauntlet full in the face of the world.” That poem goes on to add (translated):
Then will I wander god-like and victorious
through the ruins of the world.
and, giving my words an active force,
I will feel equal to the Creator.”
Marx was irresponsible, egotistical, and a thoroughly despicable human. But none of that makes Marx a bad scientist, or Marxism a bad science.
So let me start over.
Marx was not the first to embrace the Labor Theory of Value. David Ricardo and Adam Smith preceded him there. Marx was more certain than Smith that value was solely determined by the amount of manual labor it took to produce a thing plus the cost of the raw materials that went into it. Given his obscurant writing style, Marx was surprisingly clear in describing his own theory of value:
“The determination of price by the cost of production is equivalent to the determination of price by the labor time necessary for the manufacture of a commodity, for the cost of production consists of 1) raw materials and depreciation of instruments, that is, of industrial products the production of which has cost a certain amount of labor days and which, therefore, represent a certain amount of labor time, and 2) direct labor, the measure of which is, precisely, time.” – Wage Labor and Capital, 1847.
Marx undoubtedly had access to the first wave of the Austrian school of economics, but he ignored it rather than disputing it – rather like his present academic progenitors. Marx didn’t invite criticism or disputation and rarely responded to his critics. Instead he continued for decades to spew more from the same fountain, muddying the water to make it look deep. When Engels suggested to Marx that his theory of value might be misunderstood by those not accustomed to abstract thought, Marx replied, in his usual style rather than with the relative clarity of the above definition:
“. . . the conversion of surplus value into profit … presupposes a previous account of the process of circulation of capital, since the turnover of capital, etc., plays a part here. Hence this matter can be set forth only in the third book…. Here it will be shown whence the way of thinking of the philistine and the vulgar economist derives, namely, from the fact that only the immediate form in which relationships appear is always reflected in their brain, and not their inner connections. If the latter were the case, moreover, what would be the need for a science at all? If I were to silence all such objections in advance, I should ruin the whole dialectical method of development. On the contrary, this method has the advantage of continually setting traps for these fellows which provoke them to untimely demonstrations of their asininity.”
I enjoy the above quote, because in it he obfuscates his own defense of obfuscation. Some might be wondering what this idiot could really mean. The modern Marxist invariably responds that if you don’t agree with Marx, you’re not intelligent enough to understand him. Marx was no idiot. He was a skilled rhetorician who had terrible values and was profoundly dishonest. He wrote gibberish for the same reason that social scientists write it – to sound intelligent in the midst of others doing the same thing and to dupe impressionable youth. He wrote this intellectual twaddle on purpose.
Intellectuals, particularly academic ones, as Friedrich Hayek often noted, tend to overvalue intellectualism. But pseudo-intellectuals overvalue pseudo-intellectuals even more, and they have come to occupy of our academic institutions.
A favorite passage of mine comes from the Communist Manifesto, written by Marx and Engels in 1848:
“It has been objected that upon the abolition of private property, all work will cease, and universal laziness will overtake us. According to this, bourgeois society ought long ago to have gone to the dogs through sheer idleness; for those of its members who work, acquire nothing, and those who acquire anything do not work. The whole of this objection is but another expression of the tautology: that there can no longer be any wage-labor when there is no longer any capital.”
Charitably read, Marx means rich folk don’t know what work is. He seems to have no clue that some of the bourgeois’ wealth stems from putting capital at risk to predict future demand, which may involve some sort of work, sweat and misery. In fact, Marx does have such a clue, but he doesn’t want his reader to. Go back to writing poetry, you sot. It was bad, but at least it was honest.
Why should I bother analyzing Marxism as a science if no one today thinks Marxism to be a science? Ah, but they do. They just don’t write it down. It remains implicit.
Astrology and Creation Science do microscopically small harm compared to the science of Marxism. Academics routinely describe our era as “Late Capitalism,” seemingly a blind-faith acceptance of Marx’s assertion that capitalism would give rise to socialism and then communism. Thus late capitalism seems for them to be not merely an empirical fact but something axiomatic like a law of nature. Everything that comes out of university “theory” disciplines reeks of Marx’s obscurant form of expression.
Marxist-isms include modes of production, relations of production, wage-labor, social production, equivalent form, cultural hegemony, social consciousness, base and superstructure, discourse, commodity fetish, social division of labor, political economy, relative deprivation, and my favorite, theory and practice. That last phrase is so ubiquitous that, even in disciplines that feign being objective, it is shamelessly vomited out as if it would be vulgar to ask if any evidence validating said theory was ever collected prior to its being put into practice.
Nothing is really wrong with many of Marxism’s terms. Cultural hegemony can, if applied well, point to something observable in the real world. But academics across the social sciences, unfortunately often including economics, pack Marxian phraseology so tightly that not even vague meaning can be extracted.
If you’re not familiar with Marx, consider a few lines from the preface to A Contribution to the Critique of Political Economy before I move on to the havoc he has wreaked or wrought upon academia:
In the social production of their life, men enter into definite relations that are indispensable and independent of their will, relations of production which correspond to a definite stage of development of their material productive forces. The sum total of these relations of production constitutes the economic structure of society, the real foundation, on which rises a legal and political superstructure and to which correspond definite forms of social consciousness.
The mode of production of material life conditions the social, political and intellectual life process in general. It is not the consciousness of men that determines their being, but, on the contrary, their social being that determines their consciousness.
At a certain stage of their development, the material productive forces of society come in conflict with the existing relations of production, or — what is but a legal expression for the same thing — with the property relations within which they have been at work hitherto. From forms of development of the productive forces these relations turn into their fetters.
Obscurantism: muddying the water to make it look deep. He sneers at the reader, like his social-science descendants. The wording limits further inquiry to shield the writer from having the vacuousness of his content exposed. As Schopenhauer wrote of Hegel in On the Basis of Morality, “a colossal piece of mystification … by the most outrageous misuse of language, putting in its place the hollowest, most senseless, thoughtless, and, as is confirmed by its success, most stupefying verbiage” [emphasis added]. While Marx criticized Hegel’s philosophy, he loved his dialectical method and obscurant manner of expression. Such expression may work for abstract philosophical concepts but does not work in the realm of evidence, empiricism, theory selection, and theory confirmation.
Skip forward 150 years and consider the writings of modern academic Marxists, some who claim that title, others not. Judith Butler is the poster child for writing bullshit, but her stench is only slightly worse than most. Here’s her celebrated classic from the journal Diacritics in 1997:
The move from a structuralist account in which capital is understood to structure social relations in relatively homologous ways to a view of hegemony in which power relations are subject to repetition, convergence, and rearticulation brought the question of temporality into the thinking of structure, and marked a shift from a form of Althusserian theory that takes structural totalities as theoretical objects to one in which the insights into the contingent possibility of structure inaugurate a renewed conception of hegemony as bound up with the contingent sites and strategies of the rearticulation of power.
It’s not impossible to decipher this, but I think my above criticism stands. There is much less there than meets the eye. Butler replied to her critics that demands for intelligibility are aggressions intended to force her into conformity and that her shockingly radical thought simply cannot be contained by ordinary language. Mind you, Butler is not a Marxist. She just writes like one. The journal International Socialism draws a line: “Judith Butler is not a Marxist, but many of her concerns are ours too.” See also: Judith Butler’s Scientific Revolution: Foundations for a Transsexual Marxism.
Radical thought, Butler teaches, simply can’t be expressed clearly. So, when in the course of human events, it becomes necessary for one people to dissolve the political bands which have connected them with another, their only recourse shall be to rearticulate their ideological apparatus to reject structural totalities as theoretical objects with consequent commutation to those in which the insights into the contingent possibility of structure inaugurate a renewed conception of hegemony, not conceived in liberty, but bound up with the contingent strategies of the rearticulation of power.
Karl Marx, this bullshit is all on you. Your fault. I hope your hell is to listen to Judith Butler on endless replay. Better yet, Judith Butler doing an impersonation of Hegel. But then you’d probably like that. So instead, may you listen to Hemingway tape loops. Hemingway leaned Marxist. Yes. I know that. He didn’t write Marxist. He wrote well. It’s simple. Everyone knows it. I like Hemingway. The sun also rises. Isn’t it pretty to think so?
I’m going to need to start again…
Marxism: Claims to Scientific Status
Karl Marx was keenly interested in science. He claimed scientific objectivity for his theory. In Capital, for example, Marx compares himself to physicists and biologists, repeatedly characterizing his method as scientific in the same sense as those disciplines. Today’s Marxism also holds that it is a science. Marxists.org teaches that “Marxism is understood as scientific in the sense that it has understood correctly the laws of motion of a historical process taking place independently of men’s will.” It adds that all that is left for Marxists to do “is to fill in the details, to apply the scientific understanding of history.” Marxist.com (are they the for-profit alternative to Marxists.org?) teaches that “Marxism is distinguished by utilising all the developments of scientific method and historical analysis.”
My critique of modern Marxist science deals with Marxism, not Marx. Marxism relates to Marx in the way that Kuhnianism relates to Kunn: “I am not a Kuhnian,” Kuhn wrote.
“I am not a Marxist,” Marx wrote in an 1883 letter to the French Marxists, Paul Lafargue and Jules Guesde. Yet it seems impossible to leave Karl Marx out of discussion of the scientific status of Marxism or Marxian thought, because today’s Marxism still speaks in the language of Marx and Hegel. See above.
I won’t argue that Hegel has no value. But Hegel has no scientific value. Marx and Marxists put their science in the language of Hegel. See the problem?
“Reason… is Substance, as well as Infinite Power; its own Infinite Material underlying all the natural and spiritual life which it originates, as also the Infinite Form, – that which sets this Material in motion” – Hegel, Lectures on the Philosophy of World History.
Marx’s non-standard conception of evidence and scientific method is revealed in his writing:
“Scientific truth is always a paradox, if judged by everyday experience, which catches only the delusive appearance of things.” – Value, Price, and Profit, 1865
“All science would be superfluous, if the appearance, the form, and the nature of things were wholly identical.” – Capital, 1909
[Samuel Bailey] confuses the form of capital with capital itself – Capital, 1909
While Marx claimed to be following Darwin in his approach, quotes like the above make Marx seem to operate in the Platonic realm, not the scientific. Like Plato, Rousseau, and Descartes, Marx is entrenched in Theory, the sort of theory that no amount of evidence can refute, the world of Judith Butler.
Criteria of Scientificness
From the perspective of history and philosophy of science, in asking whether Marxism is good science, we need to look at its goals, claims, methods, research agenda, and explanatory ambitions. Marxism makes bold epistemic claims and gushes with explanatory aspirations. Its predictive success is an entirely different matter, and one that grabbed young Karl Popper’s attention.
Popper is the philosopher science, mentioned in the last few posts, most celebrated by modern scientists. He treated scientists as almost heroic. He thought that they court refutation by making falsifiable claims and predictions while continually putting their theories on trial. Lakatos and Popper used the term rational reconstruction to describe a hypothetical, abbreviated route between formulation of a theory and its justification. I.e., what matters to science is not the actual historical route with all the wrong turns and dead ends, but a route that could logically have been taken. As such, rational reconstruction lets us verify or vindicate theories after the fact.
Kuhn strongly disagreed with Popper that scientists put their theories on trial. Kuhn also saw it as a problem that science is taught as if the process of theory discovery and development was actually its rational reconstruction.
As a boy Popper had worked for the Communist Party and toyed with Marxism. Quickly disillusioned, he later compared the claims of Marx and Freud with those of Einstein. Popper concluded that Einstein made bold, falsifiable predictions while Marx and Freud made mostly vague predictions. Further, Einstein’s theories predicted things that defied common sense. The claims of Einstein’s theories, though unprovable for all cases, could be tested and found false in some cases, and therefore the theories could be disproven. If the rays from a distant star did not bend around the sun – a very nonintuitive effect – Einstein’s theory of gravity would be proven wrong. Was there an analog in the theories of Marx and Freud?
Marxism and Freudian psychology were held by the Vienna Circle, where Popper came of age, to be the scientific descendants of Darwinism. Popper thought Freud explained too many results – aggressive personality, shy personality, or comedian, for example – with the same cause, an abusive mother, for example. Popper thought that evidence that confirmed a theory was too easy to come by, but offered that “The criterion of the scientific status of a theory is its falsifiability” (Logic of Scientific Discovery, 1934).
He thought the Marxists made some falsifiable predictions, like that a revolution would occur in an industrialized country. But, Popper thought, those predictions were in fact falsified. Marxist predictions failed time after time. Thomas Sowell reports 40 failed predictions (yet see, e.g., “Capitalism is Unfolding Exactly as Karl Marx Predicted”). Revolutions occurred in peasant lands and not in industrial ones. Yet, in Popper’s view, on each such occasion, a post hoc revision was made by the Marxists to save their theory. The Marxists offered that if they had remembered to take into account the charisma of Lenin, then of course they would have predicted a revolution in Russia. Popper thought the Marxists continually modified their theories in the face of counterevidence, every time they were found to make wrong predictions. The result was that Marxist theories were also immune to possible falsification. For Popper, Marxism was pseudoscience.
Responses to Popper
Maurice Cornforth’s 1968 Reply to Dr. Karl Popper’s Refutations of Marxism consumes 381 pages and is similar to other Marxist responses. It contains the word evidence 14 times, theory 338 times, and revolution 170 times. In my view, a look at the points on which Conforth and Popper agree and disagree confirms Popper’s conclusions. In the passage below, Conforth agrees that science proceeds by making falsifiable theories but then adds that every scientific theory consists of more than that by resting on its fundamental theory and “is guided by it in its inquiries.”
The scrutiny of Marx’s fundamental ideas about society reveals, then, their scientific character. Dr. Popper’s failure to grasp this fact illustrates his failure, in his published work on scientific method, to grasp more than one single aspect of scientific procedures. He says that science proceeds by making “conjectures” which are “falsifiable”, and then devising all manner of ways of trying to falsify them. So far as it goes, that is true enough. But yet the body of scientific theory consists of more than just a collection of falsifiable conjectures which are variously revised or replaced by other conjectures as falsification actually overtakes them. Every well-developed science rests on its fundamental theory, and is guided by it in its inquiries. This is a feature of science which Dr. Popper never examines — possibly because he distrusts such expressions as “fundamental theory”, which he thinks redolent of pseudo-scientific metaphysics. (Cornforth, 1968)
On Conforth’s last point (resting on its fundamental theory and guided by it in its inquiries) I have two observations. First, a scientific theory does not rest on any particular fundamental theory. Newton’s theory of gravitation is a wrong but good scientific theory, by any standards. The fact that we can judge it wrong in light of the success of Einstein’s theory of gravitation, which is incompatible with Newton’s, does not lessen Newton’s status as a good theory. Its predictive success and explanatory power are incomparable. Newton’s theory of gravitation does not rest on its fundamental theory. It rests on generalizations inferred from evidence, i.e. laws of nature, but it is not self-justifying, which is the most charitable reading of “rest on its fundamental theory” that I can come up with.
Second, what might “guided by it [i.e., its fundamental theory] in its inquiries” mean in a scientific sense? I’m trying to interpret this charitably but am at a loss. It reads like what we see elsewhere in Marx’s and Marxian thought. Popper found “fundamental theory” to be pseudo-scientific metaphysics. Popper reached that conclusion because he couldn’t map those words onto any element or concept in his conception of scientific theories or in a theory of scientific explanations. I can’t, can you?
Private Language
Marxists’ only recourse to this challenge is one that we see often in Marxist responses to its critics: “you just don’t understand.” But it is the duty of Marxists to make sure they’re understood by those they wish to persuade or educate. Otherwise, their literature must be understood as dogma to be accepted by those who take the leap of faith – to believe a priori – and hope that some deeper understanding will follow. That makes Marxism a religion.
Even if such wording maps to specific concepts and the mapping is agreed upon by each Marxist, it exists as private language, and all of Wittgenstein’s concerns apply. Most centrally, if Marxism is in principle incapable of translation into ordinary language, then it can refer only to inner experiences shared by Marxists in isolation from non-Marxists. Again, this is the realm of religion, and Popper’s dogmatism critique still applies, by virtue of both belief system and language. I can find nothing that approaches a rational reconstruction of Marx’s theory or Marxist theory without the Hegelian windiness and circularity. Doctrinal disputes have always plagued Marxism, as reported even by Lenin and Stalin.
In response to Popper’s claim that Marxists continually invent supplemental hypotheses to modify their theory in light of failed predictions, Conforth, as does marxists.org, simply denies that Marxists do this: “the Marxist procedure has never been to invent supplementary hypotheses.”
Conforth admits outright that the theory is broad (vague) enough to accommodate a predicted revolution in England that never happened and an unpredicted in Russia that did happen. If Marxism’s “fundamental theory” is simply that all historical events are explained by class struggle, then the theory is purely explanatory and contains no predictive potential. And therefore, it is not scientific. Conforth argues for the predictive success of Marxism:
We simply examine what has actually happened, which has by no means exceeded the bounds of possibility allowed by the general theory of Marxism, and find that it has led to consequences predictable and accountable within the theory. And similarly with the Russian Revolution. (Cornforth, 1968)
Conforth, unsurprisingly, points out that all scientific theories undergo continual revision. Copernican heliocentrism bears little resemblance to Keplerian heliocentrism. Copernicus’s orbits were circular and still employed Ptolemaic epicycles. Indeed, but heliocentrism always made bold predictions, and when Einstein’s theory of gravitation disagreed with Newton’s revisions of Kepler and Copernicus, Newton’s theory was declared fundamentally wrong but still useful enough to predict the trajectories of spacecraft. Scientists who understand science do not say either that Newtonian mechanics is “true” or that Einstein’s theory is true. Contemporary Marxists may say the same of Marxism. It doesn’t claim truth but merely claims utility. More on Marxism’s utility below in Theory and Practice.
Granting that Marxist theory is not falsified by failed predictions requires us to accept that the theory is vague. Not only does it make vague predictions about revolutions, but sincere attempts at interpreting the theory draw different conclusions about where it sits on individual cases. If science, this seems like bad science. Imre Lakatos mostly argued against the scientificness of Marxism on the grounds of failed predictions. But from another perspective central to Lakatos, Marxism’s research agenda is paper thin. Like that of Creation Science, Marxist research, e.g. Marxist Institute for Research, does not involve increasingly specific subdomains but pedagogy and interpretation of current events (evidence) in light of Marxist theory.
Marxist Explanations
A Marxist might argue that predictive success is less important than explanatory power. Botany, some would say, is a legitimate science but makes relatively few predictions and its value is in its ability to explain the relationships between different species (forms, for the Marxists, kinds, for the Creation Scientists), along with their genetics, physiology and chemical processes. As an example, we might use botany to know what plants can live side by side and how to maximize their yield. Marxism might similarly claim to explain history and economics thereby telling us how to optimize manufacturing, distribution, and the economy in general. But that is not the focus of contemporary Marxism.
What does Marxism explain? Some would say it explains the impact of the ruling class on laborers or that all value derives from labor. But Marxism’s claims that the ruling class abuses workers and that labor is the sole source of value are not what scientists mean by explanations. They are Marxism’s claims of empirical evidence evidence itself – the things we would want a scientific explanation to explain.
There is a constant tension in scientific explanation to avoid going too deep into why questions. Doing so can quickly descend into metaphysics, as noted by the logical positivists and by Popper. But most historians and philosophers of science agree that why questions are still a primary goal of science and scientific explanations. A scientific explanation within Marxism might look at the decline of tire manufacturing in Akron in combination with the inflation-adjusted income of rubber company executives. On Marxists sites and in Marxist literature, studies of that sort are scarce in comparison to big-picture ideological writings denouncing capitalism and calling for a classless society.
Scientific explanations appeal to laws of nature. They historically have resorted to appeals to causation only after, in explaining a phenomenon, exhaustion of attempts to show that deductive logic applied to laws of nature necessitate – confer nomic expectability upon – the phenomenon being explained. In that sense explanation and prediction are mostly symmetrical. You can’t explain what you can’t predict. Alternate version: an economist is someone who can always explain why his last prediction was wrong.
Marx and Marxism use the term “laws of motion” in what seems to be an appeal to the status held by Newtonian mechanics. Kepler’s laws and Newton’s three laws are stated explicitly and concisely. Marx never tells us what his laws of motion are. Nor do more recent Marxists. In Late Capitalism, Ernest Mandel has a chapter titled “The Laws of Motion and the History of Capital.” In it he tells us that Marx “discovered” these laws and that they relate to one of the most complex problems of Marxist theory. Mandel is critical of Marx, and much of the chapter deals with the difference between Marx’s and Althusser’s understandings of markets. But Mandel never states or describes the laws and never bases an explanation of phenomena on the laws. He instead tells us that the dialectic method can explain decisive general connections between empirical material’s constituent abstract elements and Marx’s laws of motion. Here, in my third start on the topic of Marxism, I tried giving honest effort to doing right by Marxism. But this kind of writing calls up another of Schopenhauer’s comments on Hegel: “pseudo-philosophy paralyzing all mental powers, stifling all real thinking.”
Theory and Practice
The phrase Theory and Practice permeates Marxist writing. A charitable interpretation is something along the lines of: we don’t merely advocate this course of action, we put it into practice. But in what sense is that true. As Thomas Sowell points out, Marx’s contribution to economics can be readily summarized as zero: “Capital was a detour into a blind alley.” As for putting the Marxist utopia into practice, evidence suggests the practice doesn’t vindicate the theory. Marxists excel at comparing theoretical Marxism with as-deployed capitalism. Marxist theorists so undervalue evidence that they repeat a phrase attributed to Marx, “theory without practice is sterile,” as if it gives Marxism scientific status. Compare this to a phrase attributed to Immanuel Kant, “theory without evidence is mere intellectual play.” (The fact that both attributions may be spurious is irrelevant to the point.) Practice is not evidence, and, no, this is not merely a matter of translating German into English.
An example of Marx explicitly stating that theory can trump evidence is in an 1868 letter from Marx to Louis Kugelmann:
On the other hand, as you correctly assumed, the history of the theory certainly shows that the concept of the value relation has always been the same — more or less clear, hedged more or less with illusions or scientifically more or less definite. Since the thought process itself grows out of conditions, is itself a natural process, thinking that really comprehends must always be the same, and can vary only gradually, according to maturity of development, including the development of the organ by which the thinking is done. Everything else is drivel.
On Marx’s Labor Theory of Value, we now have the kind and volume of evidence about value that may not have been available to Karl Marx. We can grant Marx but not Marxists this concession. Today, integrated circuits clearly have value far above that of their raw materials and embodied labor. Integrated circuits, among countless other modern objects of consumption – software and data data, for example – are strong evidence that Carl Menger’s definition of value applies and that Karl Marx’s does not.
Value is nothing inherent in goods, no property of them, nor an independent thing existing by itself. It is a judgment economizing men make about the importance of goods at their disposal for the maintenance of their lives and well-being. Hence value does not exist outside the consciousness of men. (Menger, Principles of Economics, 1873)
Independent of accuracy or utility on Austrian economic theory, Menger’s claim that value is the quantitative relationship between requirements for a product and the availability of it is concise, and it is consistent with evidence from retail and wholesale markets. Evidence from modern life suggests that markets are far better at allocating people to production tasks than are individual persons in any role, corporate, governmental or otherwise. When asked what mechanism might in a communist (i.e. Marxist – by 1860 Marx used communism and socialism interchangeably) system to determine production requirements, Marx said “there would however be some sort of plan which would in some unspecified way determine what is really needed” [emphasis added].
History also seems to confirm Menger’s claim that Marx is wrong in believing that the spinning of yarn in a factory is the product of the labor of the operatives. Does Marx believe that systems of factory production are self-organizing?
Self-Organization in Markets
The concept of self-organization seems to me another primary defect of Marxian and Marxist belief. On this topic internal inconsistencies abound. Marx apparently believes that self-organization is possible in industry but impossible in markets. I.e., they deny that markets are emergent entities possessing knowledge about demand that no person holds individually. Likewise, today’s Marxists are perfectly comfortable with the concepts of self-organization, local reduction in entropy, and strong emergence – systems that possess emergent qualities not reduceable to the system’s constituents. Examples include belief in a naturally fined tuned universe, the natural formation of galaxies, and human evolution.
Yet today’s Marxists overwhelmingly reject that markets can know things that a specialist or bureaucrat cannot. Hayek expressed it well: “It is because every individual knows so little and because we rarely know which of us knows best that we trust the independent and competitive effort of many.” This, ironically, shows the capitalist to embrace a sort of collectivism that the modern Marxist, not Marx, rejects. Marxism applies the word collective to all sorts of things, but never to knowledge, perhaps because if they did they might be forced to allow that markets embody collective knowledge – a design without a designer, a design that extracts information from the world that no team of technocrats could acquire.
“Markets don’t solve everything” is a common retort (Robert Reich, 2, 3, 4, 5, 6). No one claims they do.
Conclusion
If Marxism is a science, either as Marx laid it out or as contemporary Marxists interpret it, it is a bad science. It either makes predictions that fail verification, and thus the theory is falsified, or it makes predictions so vague as to not be falsifiable. To the extent that it can be understood, it is internally inconsistent. A lack of precise language makes it difficult to understand, as is confirmed by historical factions and fragmentation of contemporary interpretations. Unlike Creation Science, Marxism generally lacks the trappings of science; it doesn’t publish scientific papers and its research agenda is thin. Its theory of value is inconsistent with pricing and price fluctuation of modern goods. Its arguments and explanations do not meet standard scientific criteria. For me, Marxism’s inconsistency on the tenability of self-organization and emergence shows a level of dogmatism sufficient to classify it as religion. An ugly religion at that. A radical aspect of the emergence after Galileo was the realization that while theories can be underdetermined by evidence, contrary evidence always trumps theory. Evidence is never disproved by theory. Modern Marxists fail to grasp this. Marxism does not merit the epistemic status that society affords to science but that academia grants to Marxism.
***
The last capitalist we hang shall be the one who sold us the rope. – Karl Marx
The offspring of privilege have dominated the leadership of Marxist movements from the days of Marx and Engels through Lenin, Mao, Castro, Ho Chi Minh – Thomas Sowell
The Left should put a moratorium on theory. – Richard Rorty
Jordan Peterson’s thought is filled with pseudo-science, bad pop psychology, and deep irrationalism. In other words, he’s full of shit. – Jacobin.com
Prayer may not be very efficient when compared to celestial mechanics, but it surely holds its own vis-a-vis some parts of economics. – Paul Feyerabend
True tragedy occurs when the idea of justice leads to the destruction of higher values – Richard Rorty
The Communist Manifesto, written by two bright and articulate young men without responsibility even for their own livelihoods—much less for the social consequences of their vision—has had a special appeal for successive generations of the same kinds of people. – Thomas Sowell
When I was a child, I spoke as a child, I felt as a child, I thought as a child: now that I have become a man, I put away childish things. 1 Cor 13:11
We require that our theories harmonize in detail with the very wide range of phenomena they seek to explain. We insist that they provide us with useful guidance rather than with rationalizations. – John R. Piece, An Introduction to Information Theory
It may be said of Socialism, therefore, that its friends recommended it as increasing equality, while its foes resisted it as decreasing liberty….The compromise eventually made was one of the most interesting and even curious cases in history. It was decided to do everything that had ever been denounced in Socialism, and nothing that had ever been desired in it…we proceeded to prove that it was possible to sacrifice liberty without gaining equality….In short, people decided that it was impossible to achieve any of the good of Socialism, but they comforted themselves by achieving all the bad. – G.K. Chesterton
Value is nothing inherent in goods, no property of them, nor an independent thing existing by itself. It is a judgment economizing men make about the importance of goods at their disposal for the maintenance of their lives and well-being. Hence value does not exist outside the consciousness of men. – Carl Menger
Popular Miscarriages of Science, part 3 – The Great Lobotomy Rush
Posted by Bill Storage in History of Science on January 25, 2024
On Dec. 16, 1960, Dr. Walter Freeman told his 12-year-old patient Howard Dully that he was going to run some tests. Freeman then delivered four electric shocks to Dully to put him out, writing in his surgery notes that three would have been sufficient. Then Freeman inserted a tool resembling an ice pick above Dully’s eye socket and drove it several inches into his brain. Dully’s mother had died five years earlier. His stepmother told Freeman, a psychiatrist, that Dully had attacked his brother, something the rest of Dully’s family later said never happened. It was enough for Freeman to diagnose Dully as schizophrenic and perform another of the thousands of lobotomies he did between 1936 and 1967.
“By some miracle it didn’t turn me into a zombie,” said Dully in 2005, after a two-year quest for the historical details of his lobotomy. His story got wide media coverage, including an NPR story called My Lobotomy’: Howard Dully’s Journey. Much of the media coverage of Dully and lobotomies focused on Walter Freeman, painting Freeman as a reckless and egotistical monster.
Weston State Hospital (Trans-Allegheny Lunatic Asylum), photo courtesy of Tim Kiser
In The Lobotomy Letters: The Making of American Psychosurgery, (2015) Mical Raz asks, “Why, during its heyday was there nearly no objection to lobotomy in the American medical community?” Raz doesn’t seem to have found a satisfactory answer.
(I’m including a lot of in-line references here, not to be academic, but because modern media coverage often disagrees with primary sources and scholarly papers on the dates, facts, and numbers of lobotomy. It appears that most popular media coverage seemed to use other current articles as their sources, rather than going to primary sources. As a trivial example, Freeman’s notes report that in Weston, WV, he did 225 lobotomies in 12 days. The number 228 is repeated in all the press on Howard Dully. This post is on the longer side, because the deeper I dug, the less satisfied I became that we have learned the right lesson from lobotomies.)
A gripping account of lobotomies appeared in Dr. Paul Offit’s (developer of the rotavirus vaccine) 2017 Pandora’s Lab. It tells of a reckless Freeman buoyed by unbridled media praise. Offit’s piece concludes with a warning about wanting quick fixes. If it seems too good to be true, it probably is.
In the 2005 book, The Lobotomist: A Maverick Medical Genius and his Tragic Quest to Rid the World of Mental Illness, Jack El-Hai gave a much more nuanced account, detailing many patients who thought their lobotomies hade greatly improved their lives. El-Hai’s Walter Freeman was on a compassionate crusade to help millions of asylum patients escape permanent incarceration in gloomy state mental institutions. El-Hai documents Freeman’s life-long postoperative commitment to his patients, crisscrossing America to visit the patients that he had crisscrossed America to operate on. Despite performing most of his surgery in state mental hospitals, Freeman always refused to operate on people in prison, against pressure from defense attorneys’ pleas to render convicts safe for release.
Contrasting El-Hai’s relatively kind assessment, the media coverage of Dully aligns well with Offit’s account in Pandora’s Lab. On researching lobotomies, opinions of the medical community, and media coverage, I found I disagreed with Offit’s characterization of the media coverage, more about which below. In all these books I saw signs that lobotomies are a perfect instance of bad science in the sense of what Thomas Kuhn and related thinkers would call bad science, so I want to dig into that here. I first need to expand on Kuhn, his predecessors, and his followers a bit.
Kuhn’s Precursors and the Kuhnian Groupies
Kuhn’s writing, particularly Structure of Scientific Revolutions, was unfortunately ambiguous. His friends, several of whom I was lucky enough to meet, and his responses to his critics tell us that he was no enemy of science. He thought science was epistemically special. But he thought science’s claims to objectivity couldn’t be justified. Science, in Kuhn’s view, was not simply logic applied to facts. In Structure, Kuhn wrote many things that had been said before, though by sources Kuhn wasn’t aware of.
Karl Marx believed that consciousness was determined by social factors and that thinking will always be ideological. Marx denied that what Francis Bacon (1561-1626) had advocated was possible. I.e., we can never intentionally free our minds of the idols of the mind, the prejudices resulting from social interactions and from our tribe. Kuhn partly agreed but thought that communities of scientists engaged in competitive peer review could still do good science.
Ludwik Fleck’s 1935 Genesis and Development of a Scientific Fact argued that science was a thought collective of a community whose members share values. In 1958, Norwood Hanson, in Patterns of Discovery, wrote that all observation is theory-laden. Hanson agreed with Marx that neutral observation cannot exist, so neither can objective knowledge. “Seeing is an experience. People see, not their eyes,” said Hanson.
Most like Kuhn was Michael Polanyi, a brilliant Polish polymath (chemist, historian, economist). In his 1946 Science, Faith and Society, Polanyi wrote that scientific knowledge was produced by individuals under the influence of the scientific collectives in which they operated. Polanyi long preceded Kuhn, who was unaware of Polanyi’s work, in most of Kuhn’s key concepts. Unfortunately, Polanyi’s work didn’t appear in English until after Kuhn was famous. An aspect of Polanyi’s program important to this look at lobotomies is his idea that competition in science works like competition in business. The “market” determines winners of competing theories based on the judgments of its informed participants. Something like a market process exists within the institutional structure of scientific research.
Kuhn’s Structure was perfectly timed to correspond to the hippie/protest era, which distrusted big pharma and the rest of science, and especially the cozy relationships between academia, government, and corporations – institutions of social and political power. Kuhn had no idea that he was writing what would become one of the most influential books of the century, and one that became the basis for radical anti-science perspectives. Some communities outright declared war on objectivity and rationality. Science was socially constructed, said these “Kuhnians.” Kuhn was appalled.
A Kuhnian Take on Lobotomies
Folk with STEM backgrounds might agree that politics and influence can affect which scientific studies get funded but would probably disagree with Marx, Fleck, and Hanson that interest, influence, and values permeate scientific observations (what evidence gets seen and how it is assimilated), the interpretation of measurements and data, what data gets dismissed as erroneous or suppressed, and finally the conclusions drawn from observations and data.
The concept of social construction is in my view mostly garbage. If everything is socially constructed, then it isn’t useful to say of any particular thing that it is socially constructed. But the Kuhnians, who, oddly, have now come to trust institutions like big pharma, government science, and Wikipedia, were right in principle that science is in some legitimate sense socially constructed, though they were perhaps wrong about the most egregious cases, then and now. The lobotomy boom seems a good fit for what the Kuhnians worried about.
If there is going to be a public and democratic body of scientific knowledge (science definition 2 above) based on scientific methods and testability (definition 1 above), some community of scientists has to agree on what has been tested and falsified for the body of knowledge to get codified and publicized. Fleck and Hanson’s positions apply here. To some degree, that forces definition 3 onto definitions 1 and 2. For science to advance mankind, the institution must be cognitively diverse, it must welcome debate and court refutation, and it must be transparent. The institutions surrounding lobotomies did none of these. Monstrous as Freeman may have been, he was not the main problem – at least not the main scientific problem – with lobotomies. This was bad institutional science, and to the extent that we have missed what was bad about it, it is ongoing bad science. There is much here to make your skin crawl that was missed by NPR, Offit’s Pandora’s Lab, and El-Hai’s The Lobotomist.
Background on Lobotomy
In 1935 António Egas Moniz (1874–1955) first used absolute alcohol to destroy the frontal lobes of a patient. The Nobel Committee called it one of the most important discoveries ever made in psychiatric medicine, and Moniz became a Nobel laureate in 1949. In two years Moniz oversaw about 40 lobotomies. He failed to report cases of vomiting, diarrhea, incontinence, hunger, kleptomania, disorientation, and confusion about time in postoperative patients who lacked these conditions before surgery. When the surgery didn’t help the schizophrenia or whatever condition it was done to cure, Moniz said the patients’ conditions had been too advanced before the surgery.
In 1936 neurologist Walter Freeman, having seen Moniz’s work, ordered the first American lobotomy. James Watts of George Washington University Hospital performed the surgery by drilling holes in the side of the skull and removing a bit of brain. Before surgery, Freeman lied to the patient, who was concerned that her head would be shaved, about the procedure. She didn’t consent, but her husband did. The operation was done anyway, and Freeman declared success. He was on the path to stardom.
The patient, Alice Hammatt, reported being happy as she recovered. A week after the operation, she developed trouble communicating, was disoriented, and experienced anxiety, the condition the lobotomy was intended to cure. Freeman presented the case at a medical association meeting, calling the patient cured. In that meeting, Freeman was surprised to find that he faced criticism. He contacted the local press and offered an exclusive interview. He believed that the press coverage would give him a better reception at his next professional lobotomy presentation.
By 1952, 18,000 lobotomies had been performed in the US, 3000 of which Freeman claimed to have done. He began doing them himself, despite having no training in surgery, after Watts cut ties because of Freeman’s lack of professionalism and sterilization. Technically, Freeman was allowed to perform the kind of lobotomies he had switched to, because it didn’t involve cutting. Freeman’s new technique involved using a tool resembling an ice pick. Most reports say it was a surgical orbitoclast, though Freeman’s son Frank reported in 2005 that his father’s tool came right out their kitchen cabinet. Freeman punched a hole through the eye sockets into the patient’s frontal lobes. He didn’t wear gloves or a mask. West Virginians received a disproportionate share of lobotomies. At the state hospital in Weston, Freeman reports 225 lobotomies in twelve days, averaging six minutes per procedure. In The Last Resort: Psychosurgery and the Limits of Medicine (1999), JD Pressman reports a 14% mortality rate in Freeman’s operations.
The Press at Fault?
The press is at the center of most modern coverage of lobotomies. In Pandora’s Lab, Offit, as in other recent coverage, implies that the press overwhelmingly praised the procedure from day one. Offit reports that a front page article in the June 7, 1937 New York Times “declared – ‘in what read like a patent medicine advertisement – that lobotomies could relieve ‘tension apprehension, anxiety, depression, insomnia, suicidal ideas, …’ and that the operation ‘transforms wild animals into gentle creatures in the course of a few hours.’”
I read the 1937 Times piece as far less supportive. In the above nested quote, The Times was really just reporting the claims of the lobotomists. The headline of the piece shows no such blind faith: “Surgery Used on the Soul-Sick; Relief of Obsessions Is Reported.” The article’s subhead reveals significant clinical criticism: “Surgery Used on the Soul-Sick Relief of Obsessions Is Reported; New Brain Technique Is Said to Have Aided 65% of the Mentally Ill Persons on Whom It Was Tried as Last Resort, but Some Leading Neurologists Are Highly Skeptical of It.”
The opening paragraph is equally restrained: “A new surgical technique, known as “psycho-surgery,” which, it is claimed, cuts away sick parts of the human personality, and transforms wild animals into gentle creatures in the course of a few hours, will be demonstrated here tomorrow at the Comprehensive Scientific Exhibit of the American Medical Association…“
Offit characterizes medical professionals as being generally against the practice and the press as being overwhelmingly in support, a portrayal echoed in NPR’s 2005 coverage. I don’t find this to be the case. By Freeman’s records, most of his lobotomies were performed in hospitals. Surely the administrators and staff of those hospitals were medical professionals, so they couldn’t all be against the procedure. In many cases, parents, husbands, and doctors ordered lobotomies without consent of the patient, in the case of institutionalized minors, sometimes without consent of the parents. The New England Journal of Medicine approved of lobotomy, but an editorial in the 1941 Journal of American Medical Association listed the concerns of five distinguished critics. As discussed below, two sub-communities of clinicians may have held opposing views, and the enthusiasm of the press has been overstated.
In a 2022 paper, Lessons to be learnt from the history of lobotomy, Oivind Torkildsen of the Department of Clinical Medicine at University of Bergen wrote that “the proliferation of the treatment largely appears to have been based on Freeman’s charisma and his ability to enthuse the public and the news media.” Given that lobotomies were mostly done in hospitals staffed by professionals ostensibly schooled in and practicing the methods of science, this seems a preposterous claim. Clinicians would not be swayed by tabloids.
A 1999 article by GJ Diefenbach in the Journal of the History of the Neurosciences, Portrayal of Lobotomy in the Popular Press: 1935-1960, found that the press initially used uncritical, sensational reporting styles, but became increasingly negative in later years. The article also notes that lobotomies faced considerable opposition in the medical community. It concluded that popular press may have been a factor influencing the quick and widespread adoption of lobotomy.
The article’s approach was to randomly distribute articles to two evaluators for quantitative review. The reviewers then rated the tone of the article on a five-point scale. I plotted its data, and a linear regression (yellow line below) indeed shows that the non-clinical press cooled on lobotomies from 1936 to 1958 (though, as is apparent from the broad data scatter, linear regression doesn’t tell the whole story). But the records, spotty as they are, of when the bulk of lobotomies were performed should also be considered. Of the 20,000 US lobotomies, 18,000 of them were done in the 5-year period from 1948 to 1952, the year that phenothiazines entered psychiatric clinical trials. A linear regression of the reviewers’ judgements over that period (green line) shows little change.
Applying the Methods of History and Philosophy of Science
One possibility for making sense of media coverage in the time, the occurrence of lobotomies, and the current perception of why lobotomies persisted despite opposition in the medical community is to distinguish between lobotomies done in state hospitals from those done in private hospitals or psychiatrists’ offices. The latter category dominated the press in the 1940s and modern media coverage. The tragic case of Rosemary Kennedy, whose lobotomy left her institutionalized and abandoned by her family and that of Howard Dully are far better known that the 18,000 lobotomies done in American asylums. Americans were not as in love with lobotomies as modern press reports. The latter category, private hospital lobotomies, while including some high-profile cases, was small compared to the former.
Between 1936 and 1947, only about 1000 lobotomies had been performed in the US, despite Howard Freeman’s charisma and self-promotion. We, along with Offit and NPR, are far too eager to assign blame to Howard Freeman the monster than to consider that the relevant medical communities and institutions may have been monstrous by failing to critically review their results during the lobotomy boom years.
This argument requires me to reconcile the opposition to lobotomies appearing in medical journals from 1936 on with the blame I’m assigning to that medical community. I’ll start by noting that while clinical papers on lobotomy were plentiful (about 2000 between 1936 and 1952), the number of such papers that addressed professional ethics or moral principles was shockingly small. Jan Frank, in Some Aspects of Lobotomy (Prefrontal Leucotomy) under Psychoanalytic Scrutiny (Psychiatry 13:1, 1950) reports a “conspicuous dearth of contributions to the theme.” Constance Holden, in Psychosurgery: Legitimate Therapy or Laundered Lobotomy? (Science, Mar. 16, 1973), concluded that by 1943, medical consensus was against lobotomy, and that is consistent with my reading of the evidence.
Enter Polanyi and the Kuhnians
In 2005, Dr. Elliot Valenstein (1923-2023), 1976 author of Great and Desperate Cures: The Rise and Decline of Psychosurgery, in commenting on the Dully story, stated flatly that “people didn’t write critical articles.” Referring back to Michael Polanyi’s thesis, the medical community failed itself and the world by doing bad science – in the sense that suppression of opposing voices, whether through fear of ostracization or from fear of retribution in the relevant press, destroyed the “market’s” ability to get to the truth.
By 1948, the popular lobotomy craze had waned, as is shown in Diefenbach’s data above, but the institutional lobotomy boom had just begun. It was tucked away in state mental hospitals, particularly in California, West Virginia, Virginia, Washington, Ohio, and New Jersey.
Jack Pressman, in Last resort: Psychosurgery and the Limits of Medicine (1998), seems to hit the nail on the head when he writes “the kinds of evaluations made as to whether psychosurgery worked would be very different in the institutional context than it was in the private practice context.”
Doctors in asylums and mental hospitals lived in a wholly different paradigm from those in for-profit medicine. Funding in asylums was based on patient count rather than medical outcome. Asylums were allowed to perform lobotomies without the consent of patients or their guardians, to whom they could refuse visitation rights.
While asylum administrators usually held medical or scientific degrees, their roles as administrators in poorly funded facilities altered their processing of the evidence on lobotomies. Asylum administrators had a stronger incentive than private practices to use lobotomies because their definitions of successful outcome were different. As Freeman wrote in a 1957 follow-up of 3000 patients, lobotomized patients “become docile and are easier to manage”. Success in the asylum was not a healthier patient, it was a less expensive patient. The promise of a patient’s being able to return to life outside the asylum was a great incentive for administrators on tight budgets. If those administrators thought lobotomy was ineffective, they would have had no reason to use it, regardless of their ethics. The clinical press had already judged it ineffective, but asylum administrators’ understanding of effectiveness was different from that of clinicians in private practice.
Pressman cites the calculus of Dr. Mesrop Tarumianz, administrator of Delaware State Hospital: “In our hospital, there are 1,250 cases and of these about 180 could be operated on for $250 per case. That will constitute a sum of $45,000 for 180 patients. Of these, we will consider that 10 percent, or 18, will die, and a minimum of 50 percent of the remaining, or 81 patients will become well enough to go home or be discharged. The remaining 81 will be much better and more easily cared for the in hospital… That will mean a savings $351,000 in a period of ten years.”
The point here is not that these administrators were monsters without compassion for their patients. The point is that significant available evidence existed to conclude that lobotomies were somewhere between bad and terrible for patients, and that this evidence was not processed by asylum administrators in the same way it was in private medical practice.
The lobotomy boom was enabled by sensationalized headlines in the popular press, tests run without control groups, ridiculously small initial sample sizes, vague and speculative language by Moniz and Freeman, cherry-picked – if not outright false – trial results, and complacence in peer review. Peer review is meaningless unless it contains some element of competition.
Some might call lobotomies a case of conflict of interest. To an extent that label fits, not so much in the sense that anyone derived much personal benefit in their official capacity, but in that the aims and interests of the involved parties – patients and clinicians – were horribly misaligned.
The roles of asylum administrators – recall that they were clinicians too – did not cause them to make bad decisions about ethics. Their roles caused and allowed them to make bad decisions about lobotomy effectiveness, which was an ethics violation because it was bad science. Different situations in different communities – private and state practices – led intelligent men, interpreting the same evidence, to reach vastly different conclusions about pounding holes in people’s faces.
It will come as no surprise to my friends that I will once again invoke Paul Feyerabend: if science is to be understood as an institution, there must be separation of science and state.
___
Epilogical fallacies
A page on the official website the Nobel prize still defends the prize awarded to Moniz. It uncritically accepts Freeman’s statistical analysis of outcomes, e.g., 2% of patients became worse after the surgery.
…
Wikipedia reports that 60% of US lobotomy patients were women. Later in the same article it reports that 40% of US lobotomies were done on gay men. Thus, per Wikipedia, 100% of US male lobotomy patients were gay. Since 18,000 of the 20,000 lobotomies done in the US were in state mental institutions, we can conclude that mental institutions in 1949-1951 overwhelmingly housed gay men. Histories of mental institutions, even those most critical of the politics of deinstitutionalization, e.g. Deinstitutionalization: A Psychiatric Titanic, do not mention gay men.
…
Elliot Valenstein, cited above, wrote in a 1987 Orlando Sentinel editorial that all the major factors that shaped the lobotomy boom are still with us today: “desperate patients and their families still are willing to risk unproven therapies… Ambitious doctors can persuade some of the media to report untested cures with anecdotal ‘research’… it could happen again.” Now let’s ask ourselves, is anything equivalent going on today, any medical fad propelled by an uncritical media and single individual or small cadre of psychiatrists, anything that has been poorly researched and might lead to disastrous outcomes? Nah.
Extraordinary Miscarriages of Science, Part 2 – Creation Science
Posted by Bill Storage in History of Science on January 21, 2024
By Bill Storage, Jan. 21, 2024
Creation Science can refer either to young-earth or old-earth creation theories. Young Earth Creationism (YEC) makes specific claims about the creation of the universe from nothing, the age of the earth as inferred from the Book of Genesis and about the creation of separate “kinds” of creatures. Wikipedia’s terse coverage, as with Lysenkoism, brands it a pseudoscience without explanation. But YEC makes bold, falsifiable claims about biology and genetics (not merely evolution), geology (plate tectonics or lack thereof), and, most significantly, Newtonian mechanics. While it posits unfalsifiable unobservables including a divinity that sculpts the universe in six days, much of its paradigm contrasts modern physics in testable ways. Creation Science is not a miscarriage of science in the sense of some of the others. I’m covering it here because it has many similarities to other bad sciences and is a great test of demarcation criteria. Creation Science does limited harm because it preaches to the choir. I doubt anyone ever joined a cult because they were persuaded that creationism is scientific.
Intelligent Design
Old-earth creationism, now known as Intelligent Design (ID) theory is much different. While ID could have confined itself to the realm of metaphysics and stayed out of our cross hairs, it did not. ID mostly confines itself to the realm of descriptions and explanations, but it explicitly claims to be a science. Again, Wikipedia brands ID as pseudoscience, and, again, this distinction seems shallow. I’m also concerned that the label is rooted in anti-Christian bias with reasons invented after the labelling as a rationalization. To be clear, I see nothing substantial in ID that is scientific, but its opponents’ arguments are often not much better than those of its proponents.
It might be true that a supreme being, benevolent or otherwise, guided the hand of cosmological and biological evolution. But simpler, adequate explanations of those processes exist outside of ID, and ID adds no explanatory power to the theories of cosmology and biology that are independent of it. This was not always the case. The US founding fathers, often labeled Christian by modern Christians, were not Christian at all. They were deists, mainly because they lacked a theoretical framework to explain the universe without a creator, who had little interest in earthly affairs. They accepted the medieval idea that complex organisms, like complex mechanisms, must have a designer. Emergent complexity wasn’t seen as an option. That they generally – notably excepting David Hume – failed to see the circularity of this “teleological argument” can likely be explained by Kuhn’s notion of the assent of the relevant community. Each of them bought it because they all bought it. It was the reigning paradigm.
While intelligent design could logically be understood to not require a Judeo-Christian god, ID seems to have emerged out of fundamentalist Christian objection to teaching evolution in public schools. Logically, “intelligent design” could equally apply to theories involving a superior but not supreme creator or inventor. Space aliens may have seeded the earth with amino acids – the Zoo Hypothesis. Complex organic molecules could have been sent to earth on a comet by highly advanced – and highly patient – aliens, something we might call directed panspermia. Or we could be living in a computer simulation of an alien school kid. Nevertheless, ID seems to be a Christian undertaking positing a Christian God.
Opponents are quick to point this out. ID is motivated by Christian sentiments and is closely aligned with Christian evangelism. Is this a fair criticism of ID as a science? I tend to think not. Newton was strongly motivated by Christian beliefs, though his religion, something like Arianism or Unitarianism, would certainly be rejected by modern Christians. Regardless, Newton’s religious motivation for his studies no more invalidates them than Linus Pauling’s (covered below) economic motivations invalidate his work. Motivations of practitioners, in my view, cannot be grounds for calling a field of inquiry pseudoscience or bad science. Some social scientists disagree.
Dominated by Negative Arguments
YEC and ID writings focus on arguing that much of modern science, particularly evolutionary biology, cannot be correct. For example, much of YEC’s efforts are directed at arguing that the earth cannot be 4.5 billion years old. Strictly speaking, this ( the theory that another theory is wrong) is a difficult theory to disprove. Most scientists tend to think that disproving a theory that itself aims to disprove geology is pointless. They hold that the confirming evidence for modern geologic theory is sufficient. Karl Popper, who held that absence of disconfirmation was the sole basis for judging a theory good, would seem to have a problem with this though. YEC also holds theories defending a single worldwide flood within the last 5,000 years. That seems reasonably falsifiable, if one accepts a large body of related science including several radioactive dating techniques, mechanics of solids, denudation rate calculations, and much more.
Further, it is flawed reasoning (“false choice”) to think that exposing a failure of classical geology is support for a specific competing theory.
YEC and, perhaps surprisingly, much of ID have assembled a body of negative arguments against Darwinism, geology, and other aspects of a naturalistic worldview. Arguing that fossil evidence is an insufficient basis for evolution and that natural processes cannot explain the complexity of the eyeball are characteristically negative arguments. This raises the question of whether a bunch of negative arguments can rightly be called a science. While Einstein started with the judgement that the wave theory of light could not be right (he got the idea from Maxwell), his program included developing a bold, testable, and falsifiable theory that posited that light was something that came in discreet packages, along with predictions about how it would behave in a variety of extreme circumstances. Einsteinian relativity gives us global positioning and useful tools in our cell phones. Creationism’s utility seems limited to philosophical realms. Is lack of practical utility or observable consequences a good basis for calling an endeavor unscientific? See String Theory, below.
Wikipedia (you might guess that I find Wikipedia great for learning the discography of Miley Cyrus but poor for serious inquiries), appealing to “consensus” and “the scientific community,” judges Creation Science to be pseudoscience because creationism invokes supernatural causes. In the same article, it decries the circular reasoning of ID’s argument from design (the teleological argument). But claiming that Creation Science invokes supernatural causes is equally circular unless we’re able to draw the natural/supernatural distinction independently from the science/pseudoscience distinction. Creationists hold that creation is natural; that’s their whole point.
Ignoring Disconfirming Evidence
YEC proponents seem to refuse to allow that any amount of radioactive dating evidence falsifies their theory. I’m tempted to say this alone makes YEC either a pseudoscience or just terrible science. But doing so would force me to accept the 2nd and 3rd definitions of science that I gave in the previous post. In other words, I don’t want to judge a scientific inquiry’s status (or even the status of a non-scientific one) on the basis of what its proponents (a community or institution) do at an arbitrary point in time. Let’s judge the theory, not its most vocal proponents. A large body of German physicists denied that Edington’s measurement confirmed Einstein’s prediction of bent light rays during an eclipse because they rejected Jewish physics. Their hardheadedness is no reason to call their preferred wave theory of light a bad theory. It was a good theory with bad adherents, a good theory for which we now have excellent reasons to judge wrong.
Some YEC proponents hold that, essentially, the fossil record is God’s little joke. Indeed it is possible that when God created the world in six days a few thousand years ago he laid down a lot of evidence to test our faith. The ancient Christian writer Tertullian argued that Satan traveled backward in time to plant evidence against Christian doctrine (more on him soon). It’s hard to disprove. The possibility of deceptive evidence is related to the worry expressed by Hume and countless science fiction writers that the universe, including fossils and your memories of today’s breakfast, could have been planted five minutes ago. Like the Phantom Time hypothesis, it cannot be disproved. Also, as with Phantom Time, we have immense evidence against it. And from a practical perspective, nothing in the future would change if it were true.
Lakatos Applied to Creation Science
Lakatos might give us the best basis for rejecting Creation Science as pseudoscience rather than as an extraordinarily bad science, if that distinction has any value, which it might in the case of deciding what can be taught in elementary school. (We have no laws against unsuccessful theories or poor science.) Lakatos was interested in how a theory makes use of laws of nature and what its research agenda looks like. Laws of nature are regularities observed in nature so widely that we assume them to be true, contingently, and ground predictions about nature on them. Creation Science usually has little interest in making testable predictions about nature or the universe on the basis of such laws. Dr. Duane Gish of the Institute for Creation Research (ICR) wrote in Evolution, The Fossils Say No that “God used processes which are not now operating anywhere in the natural universe.” This is a major point against Creation Science counting as science.
Creation Science’s lack of testable predictions might not even be a fair basis for judging a pursuit to be unscientific. Botany is far more explanatory than predictive, and few of us, including Wikipedia, are ready to expel botany from the science club.
Most significant for me, Lakatos casts doubt on Creation Science by the thinness of its research agenda. A look at the ICR’s site reveals a list of papers and seminars all by PhDs and MDs. They seem to fall in two categories: evolution is wrong (discussed above), and topics that are plausible but that don’t give support for creationism in any meaningful way. The ploy here is playing a game with the logic of confirmation.
By the Will of Elvis
Consider the following statement of hypothesis. Everything happens by the will of Elvis. Now this statement, if true, logically ensures that the following disjunctive statement is true: Either everything happens by the will of Elvis or all cats have hearts. Now let’s go out with a stethoscope and do some solid cat science to gather empirical evidential support for all cats having hearts. This evidence gives us reasonable confidence that the disjunctive statement is true. Since the original simple hypothesis logically implies the disjunction, evidence that cats have hearts gives support for the hypothesis that everything happens by the will of Elvis. This is a fun game (like Hempel’s crows) in the logic of confirmation, and those who have studied it will instantly see the ruse. But ICR has dedicated half its research agenda to it, apparently to deceive its adherents.
The creationist research agenda is mostly aimed at negating evolution and at large philosophical matters. Where it deals with small and specific scientific questions – analogous to cat hearts in the above example – the answers to those questions don’t in any honest sense provide evidentiary support for divine creation.
If anything fails the test of being valid science, Creation Science does. Yet popular arguments that attempt to logically dismiss it from the sciences seem prejudiced or ill motivated. As discussed in the last post, fair and honest demarcation is not so simple. This may be a case where we have to take the stance of Justice Potter Stewart, who, when judging whether Lady Chatterley’s Lover was pornography, said “I shall not today attempt further to define [it], but I know it when I see it, and this is not it.”
To be continued.
Extraordinary Popular Miscarriages of Science (part 1)
Posted by Bill Storage in History of Science, Uncategorized on January 18, 2024
By Bill Storage, Jan. 18, 2024
I’ve been collecting examples of bad science. Many came from friends and scientists I’ve talked to. Bad science can cover several aspects of science depending on what one means by science. At least three very different things are called science now:
- An approach or set of rules and methods used to understand and predict nature
- A body of knowledge about nature and natural processes
- An institution, culture or community of people, including academic, government and corporate professionals, who are involved, or are said to be involved, in 1. or 2. above
Many of my examples of bad science fall under the 3rd category and involve, or are dominated by, the academicians, government offices, and corporations. Below are a few of my favorites from the past century or so. I think many people tend to think that bad science happened in medieval times and that the modern western world is immune to that sort of thing. On the contrary, bad science may be on the rise. For the record, I don’t judge a theory bad merely because it was shown to be wrong, even if spectacularly wrong. Geocentricity was a good theory. Phlogiston (17th century theoretical substance believed to escape from matter during combustion), caloric theory (18th century theory of a weightless fluid that flows from hot matter to cold), and the luminiferous ether (17-19th century postulated medium for the propagation of light waves) were all good theories, though we now have robust evidence against them. All had substantial predictive power. All posited unobservable entities to explain phenomena. But predictive success alone cannot justify belief in unobservable entities. Creation science and astrology were always bad science.
To clarify the distinction between bad science and wrong theories, consider Trofim Lysenko. He was nominally a scientist. Some of his theories appear to be right. He wore the uniform, held the office, and published sciencey papers. But he did not behave scientifically (consistent with definition 1 above) when he ignored the boundless evidence and prior art about heredity. Wikipedia dubs him a pseudoscientist, despite his having some successful theories and making testable hypotheses. Pseudoscience, says Wikipedia, makes unfalsifiable claims. Lysenko’s bold claims were falsifiable, and they were falsified. Wikipedia talks as if the demarcation problem – knowing science from pseudoscience – is a closed case. Nah. Rather than tackle that matter of metaphysics and philosophy, I’ll offer that Lysenkoism, like creation science, and astrology, are all sciences but they are bad science. While they all make some testable predictions, they also make a lot of vague ones, their interest in causation is puny, and their research agendas are scant.
Good science entails testable, falsifiable theories and bold predictions. Most philosophers of science, notably excluding Karl Popper, who thought that only withstanding falsification mattered, have held that making succinct, correct prediction makes a theory good, and that successful theories make for good science. Larry Laudan gave, in my view, a fine definition of a successful theory in his 1984 Philosophy of Science: A theory is successful provided it makes substantially more correct predictions, that it leads to efficacious interventions in the natural order, or that it passes a suitable battery of tests.
Concerns over positing unobservables opens a debate on the question of just how observable are electrons, quarks, and the Higgs Field. Not here though. I am more interested in bad science (in the larger senses of science) than I am with wrong theories. Badness often stems not from seeking to explain and predict nature and failing out of refusal to read the evidence fairly, but from cloaking a non-scientific agenda in the trappings of science. I’m interested in what Kuhn, Feyerabend, and Lakatos dealt with – the non-scientific interests of academicians, government offices, and corporations and their impact on what gets studied and how it gets studied, how confirming evidence is sought and processed, how disconfirming evidence is processed, avoided, or dismissed, and whether Popperian falsifiability was ever on the table.
Recap of Kuhn, Feyerabend, and Lakatos
Thomas Kuhn claimed that normal (day-to-day lab-coat) science consisted of showing how nature can be fit into the existing theory. That is, normal science is decidedly unscientific. It is bad science, aimed at protecting the reigning paradigm from disconfirming evidence. On Kuhn’s view, your scientific education teaches you how to see things as your field requires them to be seen. He noted that medieval and renaissance astronomers never saw the supernovae that were seen in China. Europeans “knew” that the heavens were unchanging. Kuhn used the terms dogma and indoctrination to piss off scientists of his day. He thought that during scientific crises (Newton vs. Einstein being the exemplar) scientists clutched at new theories, often irrationally, and then vicious competition ended when scientific methods determined the winner of a new paradigm. Kuhn was, unknown to most of his social-science groupies, a firm believer that the scientific enterprise ultimately worked. Kuhn says normal science is bad science. He thought this was okay because crisis science reverted to good science, and in crisis, the paradigm was overthrown when the scientists got interested in philosophy of science. When Kuhn was all the rage in the early 1960s, radical sociologists of science, all at the time very left leaning, had their doubts that science could stay good under the influence of government and business. Recall worries about the military industrial complex. They thought that interest, whether economic or political, could keep science bad. I think history has sided with those sociologists; though today’s professional sociologists, now overwhelmingly employed by the the US and state governments, are astonishingly silent on the matter. Granting, for sake of argument, that social science is science, its practitioners seem to be living proof that interest can dominate not only research agendas but what counts as evidence, along with the handling of evidence toward what becomes dogma in the paradigm.
Paul Feyerabend, though also no enemy of science, thought Kuhn stopped short of exposing the biggest problems with science. Feyerabend called science, referring to science as an institution, a threat to democracy. He called for “a separation of state and science just as there is a separation between state and religious institutions.” He thought that 1960s institutional science resembled more the church of Galileo’s day than it resembled Galileo. Feyerabend thought theories should be tested against each other, not merely against the world. He called institutional science a threat because it increasingly held complete control over what is deemed scientifically important for society. Historically, he observed, individuals, by voting with their attention and their dollars, have chosen what counts as being socially valuable. Feyerabend leaned rather far left. In my History of Science appointment at UC Berkeley I was often challenged for invoking him against bad-science environmentalism because Feyerabend wouldn’t have supported a right-winger. Such is the state of H of S at Berkeley, now subsumed by Science and Technology Studies, i.e., same social studies bullshit (it all ends in “Studies”), different pile. John Heilbronn rest in peace.
Imre Lakatos had been imprisoned by the Nazis for revisionism. Through that experience he saw Kuhn’s assent of the relevant community as a valid criterion for establishing a new post-crisis paradigm as not much of a virtue. It sounded a bit too much like Nazis and risked becoming “mob psychology.” If the relevant community has excessive organizational or political power, it can put overpowering demands on individual scientists and force them to subordinate their ideas to the community (see String Theory’s attack on Lee Smolin below). Lakatos saw the quality of a science’s research agenda as a strong indicator of quality. Thin research agendas, like those of astrology and creation science, revealed bad science.
Selected Bad Science
Race Science and Eugenics
Eugenics is an all time favorite, not just of mine. It is a poster child for evil-agenda science driven by a fascist. That seems enough knowledge of the matter for the average student of political science. But eugenics did not emerge from fascism and support for it was overwhelming in progressive circles, particularly in American universities and the liberal elite. Alfred Binet of IQ-test fame, H. G. Wells, Margaret Sanger, John Harvey Kellogg, George Bernard Shaw, Theodore Roosevelt, and apparently Oliver Wendell Holmes, based on his decision that compulsory sterilization was within a state’s rights, found eugenics attractive. Financial support for the eugenics movement included the Carnegie Foundation, Rockefeller Institute, and the State Department. Harvard endorsed it, as did Stanford’s first president, David S Jordan. Yale’s famed economist and social reformer Irving Fisher was a supporter. Most aspects of eugenics in the United States ended abruptly when we discovered that Hitler had embraced it and was using it to defend the extermination of Jews. Hitler borrowed from our 1933 Law for the Prevention of Hereditarily Defective Offspring drawn up by Harry Laughlin. Eugenics was a class case of advocates and activists, clueless of any sense of science, broadcasting that the science (the term “race science” exploded onto the scene as if if had always been a thing) had been settled. In an era where many Americans enjoy blaming the living – and some of the living enjoy accepting that blame – for the sins of our fathers, one wonders why these noble academic institutions have not come forth to offer recompense for their eugenics transgressions.
The War on Fat
In 1977 a Senate committee led by George McGovern published “Dietary Goals for the United States,” imploring us to eat less red meat, eggs, and dairy products. The U.S. Department of Agriculture (USDA) then issued its first dietary guidelines, which focused on cutting cholesterol and not only meat fat but fat from any source. The National Institutes of Health recommended that all Americans, including young kids, cut fat consumption. In 1980 the US government broadcast that eating less fat and cholesterol would reduce your risk of heart attack. Evidence then and ever since has not supported this edict. A low-fat diet was alleged to mitigate many metabolic risk factors and to be essential for achieving a healthy body weight. However, over the past 45 years, obesity in the US climbed dramatically while dietary fat levels fell. Europeans with higher fat diets, having the same genetic makeup, are far thinner. The science of low-fat diets and the tenets of related institutions like insurance, healthcare, and school lunches have seemed utterly immune to evidence. Word is finally trickling out. The NIH has not begged pardon.
The DDT Ban
Rachel Carson appeared before the Department of Commerce in 1963, asking for a “Pesticide Commission” to regulate the DDT. Ten years later, Carson’s “Pesticide Commission” became the Environmental Protection Agency, which banned DDT in the US. The rest of the world followed, including Africa, which was bullied by European environmentalists and aid agencies to do so.
By 1960, DDT use had eliminated malaria from eleven countries. Crop production, land values, and personal wealth rose. In eight years of DDT use, Nepal’s malaria rate dropped from over two million to 2,500. Life expectancy rose from 28 to 42 years.
Malaria reemerged when DDT was banned. Since the ban, tens of millions of people have died from malaria. Following Rachel Carson’s Silent Spring narrative, environmentalists claimed that, with DDT, cancer deaths would have negated the malaria survival rates. No evidence supported this. It was fiction invented by Carson. The only type of cancer that increased during DDT use in the US was lung cancer, which correlated cigarette use. But Carson instructed citizens and governments that DDT caused leukemia, liver disease, birth defects, premature births, and other chronic illnesses. If you “know” that DDT altered the structure of eggs, causing bird populations to dwindle, it is Carson’s doing.
Banning DDT didn’t save the birds, because DDT wasn’t the cause of US bird death as Carson reported. While bird populations had plunged prior to DDT’s first use, the bird death at the center of her impassioned plea never happened. We know this from bird count data and many subsequent studies. Carson, in her work at Fish and Wildlife Service and through her participation in Audubon bird counts, certainly knew that during US DDT use, the eagle population doubled, and robin, dove, and catbird counts increased by 500%. Carson lied like hell and we showered her with praise and money. Africans paid with their lives.
In 1969 the Environmental Defense Fund demanded a hearing on DDT. The 8-month investigation concluded DDT was not mutagenic or teratogenic. No cancer, no birth defects. In found no “deleterious effect on freshwater fish, estuarine organisms, wild birds or other wildlife.” Yet William Ruckleshaus, first director of the EPA, who never read the transcript, chose to ban DDT anyway. Joni Mitchell was thrilled. DDT was replaced by more harmful pesticides. NPR, the NY Times, and the Puget Sound Institute still report a “preponderance of evidence” of DDT’s dangers.
When challenged with the claim that DDT never killed kids, the Rachel Carson Landmark Alliance responded in 2017 that indeed it had. A two-year old drank and ounce of 5% DDT in a solution of kerosene and died. Now there’s scientific integrity.
Vilification of Cannabis
I got this one from my dentist; I had never considered it before. White-collar, or rather, work-from-home, California potheads think this problem has been overcome. Far from it. Cannabis use violates federal law. Republicans are too stupid to repeal it, and Democrats are too afraid of looking like hippies. According to Quest Diagnostics, in 2020, 4.4% of workers failed their employers’ drug tests. Blue-collar Americans, particularly those who might be a sub-sub-subcontractor on a government project, are subject to drug tests. Testing positive for weed can cost you your job. So instead of partying on pot, the shop floor consumes immense amounts of alcohol, increasing its risk of accidents at work and in the car, harming its health, and raising its risk of hard drug use. To the admittedly small sense in which the concept of a gateway drug is valid, marijuana is probably not one and alcohol almost certainly is. Racism, big pharma lobbyists, and social-control are typically blamed for keeping cannabis illegal. Governments may also have concluded that tolerating weed at the state level while maintaining federal prohibition is an optimal tax revenue strategy. Cannabis tolerance at state level appears to have reduced opioid use and opioid related ER admissions.
Stoners who scoff at anti-cannabis propaganda like Reefer Madness might be unaware that a strong correlation between psychosis and cannabis use has been known for decades. But inferring causation from that correlation was always either highly insincere (huh huh) or very bad science. Recent analysis of study participants’ genomes showed that those with the strongest genetic profile for schizophrenia were also more likely to use cannabis in large amounts. So unless you follow Lysenko, who thought acquired traits were passed to offspring, pot is unlikely to cause psychosis. When A and B correlate, either A causes B, B causes A, or C causes both, as appears to be the case with schizophrenic potheads.
To be continued.
Settled State Science
Posted by Bill Storage in History of Science on August 15, 2022
Science is belief in the ignorance of experts, said Richard Feynman in 1969. Does that describe science today, or is science a state and/or academic institution that dispenses truth?
State science and science herded by well-funded and tenured academics has led to some mammoth missteps, muddles and misdeeds in the application of that science to policy.
It may be inaccurate to say, as Edwin Black did in War Against the Weak, that Hitlers racial hygienics ideology was imported directly and solely from American eugenics. But that Hitler’s race policy was heavily inspired by American eugenics is very well documented, as is the overwhelming support given eugenics by our reigning politicians and educators. For example, Hitler absolutely did borrow much of the 1933 Law for the Prevention of Hereditarily Defective Offspring from the draft sterilization law drawn up for US states by Harry Laughlin, then Superintendent of the Eugenics Record Office in affiliation with the American Association of the Advancement of Science (AAAS).
Academic progressives and the educated elite fawned over the brilliance of eugenics too. Race Science was deemed settled, and that science had to be embodied in policy to change the world for the better. John Maynard Keynes and Woodrow Wilson loved it. Harvard was all over it too. Stanford’s first president, David S Jordan and the Yale’s famed economist and social reformer Irving Fisher were leaders of the Eugenics movement. All the trappings of science were there; impressive titles like “Some Racial Peculiarities of the Negro Brain” (American Journal of Anatomy, 1906) appeared in sciencey journals. In fact, the prestigious journal Science, covered eugenics in it lead story of Oct. 7, 1921.
But 1906 was oh so very long ago. right? Was eugenics a one-off? The lobotomy/leucotomy craze of the 1950s saw similar endorsement from the political and academic elite. More recent, less grotesque, but equally bad and unjustified state science was the low-fat craze of the 1980s and the war on cholesterol.
Last month the California Assembly has passed AB 2098, designating “the dissemination or promotion of misinformation or disinformation related to the SARS-CoV-2 coronavirus, or COVID-19 as unprofessional conduct,” for which MDs could be subjected to loss of license. The bill defines misinformation as “false information that is contradicted by contemporary scientific consensus.”
The U.S. Department of Health & Human Services (HHS) now states, “If your child is 6 months or older, you can now help protect them from severe COVID illness by getting them a COVID vaccine.” That may be consensus alright. I cannot find one shred of evidence to support the claim. Can you?
___
“The separation of state and church must be complemented by the separation of state and science, that most recent, most aggressive, and most dogmatic religious institution.” – Paul Feyerabend, Against Method, 1975
Fashionable Pessimism: Confidence Gap Revisited
Posted by Bill Storage in Uncategorized on August 19, 2021
Most of us hold a level of confidence about our factual knowledge and predictions that doesn’t match our abilities. That’s what I learned, summarized in a recent post, from running a website called The Confidence Gap for a year.
When I published that post, someone linked to it from Hacker News, causing 9000 people to read the post, 3000 of which took the trivia quiz(es) and assigned confidence levels to their true/false responses. Presumably, many of those people learned from the post that the each group of ten questions in the survey had one question about the environment or social issues designed to show an extra level of domain-specific overconfidence. Presumably, those readers are highly educated. I would have thought this would have changed the gap between accuracy and confidence in those who used the site before and after that post. But the results from visits after the blog post and Hacker News coverage, even in those categories, were almost identical to those of the earlier group.
Hacker News users pointed out several questions where the the Confidence Gap answers were obviously wrong. Stop signs actually do have eight sides, for example. Readers also reported questions with typos that could have confused the respondents. For example “Feetwood Mac” did not perform “Black Magic Woman” prior to Santana, but Fleetwood Mac did. The site called the statement with “Feetwood” true; it was a typo, not a trick.
A Hacker News reader challenged me on the naïve averaging of confidence estimates, saying he assumed the whole paper was similarly riddled with math errors. The point is arguable, but not a math error. Philip Tetlock, Tony Cox, Gerd Gigerenzer, Sarah Lichtenstein, Baruch Fischhoff, Paul Slovic and other heavyweights of the field used the same approach I used. Thank your university system for teaching that interpretation of probability is a clear-cut matter of math as opposed to vexing issue in analytic philosophy (see The Trouble with Probability and The Trouble with Doomsday).
Those criticisms acknowledged, I deleted the response data from the questions where Hacker News reported errors and typos. This changed none of the results by more than a percentage point. And, as noted above, prior knowledge of “trick” questions had almost no effect on accuracy or overconfidence.
On the point about the media’s impact on people’s confidence about fact claims that involve environmental issues, consider data from the 2nd batch of responses (post blog post) to this question:
According to the United Nations the rate of world deforestation increased between 1995 and 2015
This statement about a claim made by the UN is false, and the UN provides a great deal of evidence on the topic. The average confidence level given by respondents was 71%. The fraction of people answering correctly was 29%. The average confidence value specified by those who answered incorrectly was 69%. Independent of different interpretations of probability and confidence, this seems a clear sign of overconfidence about deforestation facts.
Compare this to the responses given for the question of whether Oregon borders California. 88% of respondents answered correctly and their average confidence specified was 88%.
Another example:
According to OurWorldInData.org, the average number of years of schooling per resident was higher in S. Korea than in USA in 2010
The statement is false. Average confidence was 68%. Average correctness was 20%
For all environmental and media-heavy social questions answered by the 2nd group of respondents (who presumably had some clue that people tend to be overconfident about such issues) the average correctness was 46% and the average confidence was 67%. This is a startling result; the proverbial dart throwing chimps would score vastly higher on environmental issues (50% by chimps, 20% on the schooling question and 46% for all “trick” questions by humans) than American respondents who were specifically warned that environmental questions were designed to demonstrate that people think the world is more screwed up than it is. Is this a sign of deep pessimism about the environment and society?
For comparison, average correctness and confidence on all World War II questions were both 65%. For movies, 70% correct, 71% confidence. For science, 75% and 77%. Other categories were similar, with some showing a slightly higher overconfidence. Most notably, sports mean accuracy was 59% with mean confidence of 68%.
Richard Feynman famously said he preferred not knowing to holding as certain the answers that might be wrong (No Ordinary Genius). Freeman Dyson famously said, “it is better to be wrong than to be vague” (The Scientist As Rebel). For the hyper-educated class, spoon-fed with facts and too educated to grasp the obvious, it seems the preferred system might now be phrased “better wrong than optimistic.”
. . . _ _ _ . . .
The man who despairs when others hope is admired as a sage. – John Stuart Mill. Speech on Perfectibility, 1828
Optimism is cowardice. Otto Spengler, Man and Technics, 1931
The U.S. life expectancy will drop to 42 years by 1980 due to cancer epidemics. Paul Ehrlich. Ramparts, 1969
It is the long ascent of the past that gives the lie to our despair. HG Wells. The Discovery of the Future, 1902
Despising Derrida, Postmodern Scapegoat
Posted by Bill Storage in Philosophy on May 10, 2021
There is a trend in conservative politics to blame postmodernism for everything that is wrong with America today. Meanwhile conservatives say a liberal who claims that anything is wrong with the USA should be exiled to communist Canada. Postmodernism in this context is not about art and architecture. It is a school of philosophy – more accurately, criticism – that not long ago was all the rage in liberal education and seems to have finally reached business and government. Right-wing authors tie it to identity politics, anti-capitalism, anti-enlightenment and wokeness. They’re partly right.
Postmodernism challenged the foundations of knowledge, science in particular, arguing against the univocity of meaning. Postmodernists think that there is no absolute truth, no certain knowledge. That’s not the sort of thing Republicans like to hear.
Deconstruction, an invention of Jacques Derrida, was a major component of heyday postmodernism. Deconstruction dug into the fine points of the relationship between text and meaning, something like extreme hermeneutics (reading between the lines, roughly). Richard Rorty, the leading American postmodernist, argued that there can be no unmediated expression of any non-linguistic entity. And what does that mean?
It means in part that there is no “God’s eye view” or “view from nowhere,” at least none that we have access to. Words cannot really hook onto reality for several reasons. There are always interpreters between words and reality (human interpreters), and between you and me. And we really have no means of knowing whether your interpretation is the same as mine. How could we test such a thing? Only by using words on each other. You own your thoughts but not your words once they’ve left your mouth or your pen. They march on without you. Never trust the teller; trust the tale, said D.H. Lawrence. Derrida took this much farther, exploring “oppositions inside text,” which he argued, mostly convincingly, can be found in any nontrivial text. “There is nothing outside the text,” Derrida proclaimed.
Derrida was politically left but not nearly as left as his conservative enemies pretended. Communists had no use for Derrida. Conservatives outright despised him. Paul Gross and Norman Levitt spent an entire chapter deriding Derrida for some inane statements he made about Einstein and relativity back before Derrida was anyone. In Higher Superstition – The Academic Left and its Quarrels with Science, they attacked from every angle, making much of Derrida’s association with some famous Nazis. This was a cheap shot having no bearing on the quality of Derrida’s work.
Worse still, Gross and Levitt attacked the solid aspects of postmodern deconstruction:
“The practice of close, exegetical reading, of hermeneutics, is elevated an ennobled by Derrida and his followers. No longer is it seen as a quaint academic hobby-horse for insular specialists, intent on picking the last meat from the bones of Jane Austen and Herma Melville. Rather, it has now become the key to comprehension of the profoundest matters of truth and meaning, the mantic art of understanding humanity and the universe at their very foundation.”
There was, and is, plenty of room between Jane Austen hermeneutics and arrogantly holding that nothing has any meaning except that which the god of deconstruction himself has tapped into. Yes, Derrida the man was an unsavory and pompous ass, and much of his writing was blustering obscurantism. But Derrida-style deconstruction has great value. Ignore Derrida’s quirks, his arrogance, and his political views. Ignore “his” annoying scare quotes and “abuse” of “language.” Embrace his form of deconstruction.
Here’s a simple demo of oppositions inside text. Hebrews 13 tells us to treat people with true brotherly love, not merely out of adherence to religious code. “Continue in brotherly love. Do not neglect to show hospitality to strangers, for by so doing some have entertained angels without knowing it.” The Hebrews author has embedded a less pure motive in his exhortation – a favorable review from potential angels in disguise. Big Angel is watching you.
Can conservatives not separate Derrida from his work, and his good work from his bad? After all, they are the ones who think that objective criteria can objectively separate truth from falsehood, knowledge from mere belief, and good (work) from bad.
Another reason postmodernists say the distinction between truth and falsehood is fatally flawed – as is in fact the whole concept of truth – is the deep form of the “view from nowhere” problem. This is not merely the impossibility of neutrality in journalism. It is the realization that no one can really evaluate a truth claim by testing its correspondence to reality – because we have no unmediated access to the underlying reality. We have only our impressions and experience. If everyone is wearing rose colored glasses that cannot be removed, we can’t know whether reality is white or is rose colored. Thus falls the correspondence theory of truth.
Further, the coherence theory of truth is similarly flawed. In this interpretation of truth, a statement is judged likely true if it coheres with a family of other statements accepted as true. There’s an obvious bootstrapping problem here. One can imagine a large, coherent body of false claims. They hang together, like the elements of a tall tale, but aren’t true.
Beyond correspondence and coherence, we’re basically out of defenses for Truth with a capital T. There are a few other theories of truth, but they more or less boil down to variants on these two core interpretations. Richard Rorty, originally an analytic philosopher (the kind that studies math and logic and truth tables), spent a few decades poking all aspects of the truth problem, borrowing a bit from historian of science Thomas Kuhn. Rorty extended what Kuhn had only applied to scientific truth to truth in general. Experiments – and experience in the real world – only provide objective verification of truth claims if your audience (or opponents) agree that it does. For Rorty, this didn’t mean there was no truth out there, but it meant that we don’t have any means of resolving disputes over incompatible truth claims derived from real world experience. Applying Kuhn to general knowledge, Truth is merely the assent of the relevant community. Rorty’s best formulation of this concept was that truth is just a compliment we pay to claims that satisfy our group’s validation criteria. Awesome.
Conservatives cudgeled the avowed socialist Rorty as badly as they did Derrida. Dinesh D’Souza saw Rorty as the antichrist. Of course conservatives hadn’t bothered to actually read Rorty any more than they had bothered to read Derrida. Nor had conservatives ever read a word from Michel Foucault, another postmodern enemy of all things seen as decent by conservatives. Foucault was once communist. He condoned sex between adults and consenting children. I suspect some religious conservatives secretly agree. He probably had Roman Polanski’s ear. He politicized sexual identity – sort of (see below). He was a moral relativist; there is no good or bad behavior, only what people decide is good for them. Yes, Foucault was a downer and a creep, but some of his his ideas on subjectivity were original and compelling.
The conservatives who hid under their beds from Derrida, Rorty and Foucault did so because they relied on the testimony of authorities who otherwise told them what they wanted to hear about postmodernism. Thus they missed out on some of the most original insights about the limitations of what it is possible to know, what counts as sound analytical thinking, and the relationship between the teller and the hearer. Susan Sontag, an early critic of American exceptionalism and a classic limousine liberal, famously condemned interpretation. But she emptied the tub leaving the baby to be found by nuns. Interpretation and deconstruction are useful, though not the trump card the postmodernism founders originally thought they had. They overplayed their hand, but there was something in that hand.
Postmodernists, in their critique of science, thought scientists were incapable of sorting through evidence because of their social bias, their interest, as Marxists like to say. They critically examined science – in a manner they judged to be scientific, oddly enough. They sought to knock science down a peg. No objective truth, remember. Postmodern social scientists found that interest pervaded hard science and affected its conclusions. These social scientists, using scientific methods, were able to sort through interest in the way that other scientists could not sort through evidence. See a problem here? Their findings were polluted by interest.
When a certain flavor of the vegan, steeped in moral relativism, argues that veganism is better for your health, and, by the way, it is good for the planet, and, by the way, animals have rights, and, by the way, veganism is what our group of social activists do…, then I am tempted to deploy some deconstruction. We can’t know motives, some say. Or can we? There is nothing outside the text. Can an argument reasonably flow from multiple independent reasons? We can be pretty sure that some of those reasons were backed into from a conclusion received from the relevant community. Cart and horse are misconfigured.
Conservatives didn’t read Derrida, Foucault and Rorty, and liberals only made it through chapter one. If they had read further they wouldn’t now be parroting material from the first week of Postmodernism 101. They wouldn’t be playing the village postmodernist.
Foucault, patron saint of sexual identity among modern liberal academics, himself offered that to speak of homosexuals as a defined group was historically illiterate. He opined that sexual identity was an absurd basis to form one’s personal identity. They usually skip that part during protest practice. The political left in 2021 exists at the stage of postmodern thought before the great postmodernists, Derrida and crew, realized that the assertion that it is objectively true that nothing is objectively true is more than a bit self-undermining. They missed a boat that sailed 50 years back. Postmodern thought, applied to postmodernism, destroys postmodernism as a program. But today its leading adherents don’t know it. On the death of Postmodernism with a capital P we inherited some good tools and perspectives. But the present postmodern evangelists missed the point where logic flushed the postmodern program down the same drain where objective truth had gone. They are like Sunday Christians, they’re the Cafeteria Catholics of postmodernism.
Richard Rorty, a career socialist, late in his life, using postmodern reasoning, took moral relativism to its logical conclusion. He realized that the implausibility of moral absolutism did not support its replacement by moral relativism. The former could be out without the latter being in. If two tribes hold incommensurable “truths,” it is illogical for either to conclude the other is equally correct. After all, each reached its conclusion based on the evidence and what that community judged to be sound reasoning. It would be hypocritical or incoherent to be less resolved about a conclusion, merely by knowing that a group with whom you did not share moral or epistemic values, concluded otherwise. That reasoning has also escaped the academic left. This was the ironic basis for Rorty’s intellectual defense of ethnocentrism, which got him, once the most prominent philosopher in the world, booted from academic prominence, deleted from libraries, and erased from history.
Rorty’s 1970’s socialist side does occasionally get trotted out by The New Yorker to support identify politics whenever needed, despite his explicit rejection of that concept by name. His patriotic side, which emerged from his five decade pursuit of postmodern thought, gets no coverage in The New Republic or anywhere else. National pride, Rorty said, is to countries what self-respect is to individuals – a necessary condition for self-improvement. Hearing that could put some freshpersons in the campus safe place for a few days. Are the kittens ready?
Postmodern sock puppets, Derrida, Foucault, and Rorty are condemned by conservatives and loved by liberals. Both read into them whatever they want and don’t want to hear. Appropriation? Or interpretation?
Derrida would probably approve. He is “dead.” And he can make no “claim” to the words he “wrote.” There is nothing outside the text.
Smart Folk Often Full of Crap, Study Finds
Posted by Bill Storage in Uncategorized on April 22, 2021
For most of us, there is a large gap between what we know and what we think we know. We hold a level of confidence about our factual knowledge and predictions that doesn’t match our abilities. Since our personal decisions are really predictions about the future based on our available present knowledge, it makes sense to work toward adjusting our confidence to match our skill.
Last year I measured the knowledge-confidence gap of 3500 participants in a trivia game with a twist. For each True/False trivia question the respondents specified their level of confidence (between 50 and 100% inclusive) with each answer. The questions, presented in banks of 10, covered many topics and ranged from easy (American stop signs have 8 sides) to expert (Stockholm is further west than Vienna).
I ran this experiment on a website and mobile app using 1500 True/False questions, about half of which belonged to specific categories including music, art, current events, World War II, sports, movies and science. Visitors could choose between the category “Various” or from a specific category. I asked for personal information such as age, gender current profession, title, and education. About 20% of site visitors gave most of that information. 30% provided their professions.
Participants were told that the point of the game was not to get the questions right but to have an appropriate level of confidence. For example, if a your average confidence value is 75%, 75% of their your answers should be correct. If your confidence and accuracy match, you are said to be calibrated. Otherwise you are either overconfident or underconfident. Overconfidence – sometime extreme – is more common, though a small percentage are significantly underconfident.
Overconfidence in group decisions is particularly troubling. Groupthink – collective overconfidence and rationalized cohesiveness – is a well known example. A more common, more subtle, and often more dangerous case exists when social effects and the perceived superiority of judgment of a single overconfident participant can leads to unconscious suppression of valid input from a majority of team members. The latter, for example, explains the Challenger launch decision for more than classic groupthink does, though groupthink is often cited as the cause.
I designed the trivia quiz system so that each group of ten questions under the Various label included one that dealt with a subject about which people are particularly passionate – environmental or social justice issues. I got this idea from Hans Rosling’s book, Factfulness. As expected, respondents were both overwhelmingly wrong and acutely overconfident about facts tied to emotional issues, e.g., net change in Amazon rainforest area in last five years.
I encouraged people to use take a few passes through the Various category before moving on to the specialty categories. Assuming that the first specialty categories that respondents chose was their favorite, I found them to be generally more overconfident about topics they presumable knew best. For example, those that first selected Music and then Art showed both higher resolution (correctness) and higher overconfidence in Music than they did in Art.
Mean overconfidence for all first-chosen specialties was 12%. Mean overconfidence for second-chosen categories was 9%. One interpretation is that people are more overconfident about that which they know best. Respondents’ overconfidence decreased progressively as they answered more questions. In that sense the system served as confidence calibration training. Relative overconfidence in the first specialty category chosen was present even when the effect of improved calibration was screened off, however.
For the first 10 questions, mean overconfidence in the Various category was 16% (16% for males, 14% for females). Mean overconfidence for the nine question in each group excepting the “passion” question was 13%.
Overconfidence seemed to be constant across professions, but increased about 1.5% with each level of college education. PhDs are 4.2% more overconfident than high school grads. I’ll leave that to sociologists of education to interpret. A notable exception was a group of analysts from a research lab who were all within a point or two of perfect calibration even on their first 10 questions. Men were slightly more overconfident than women. Underconfidence (more than 5% underconfident) was absent in men and present in 6% of the small group identifying as women (98 total).
The nature of overconfidence is seen in the plot of resolution (response correctness) vs. confidence. Our confidence roughly matches our accuracy up to the point where confidence is moderately high, around 85%. After this, increased confidence occurs with no increase in accuracy. At at 100% confidence level, respondents were, on average, less correct than they were at 95% confidence. Much of that effect stemmed from the one “trick” question in each group of 10; people tend to be confident but wrong about hot topics with high media coverage.
The distribution of confidence values expressed by participants was nominally bimodal. People expressed very high or very low confidence about the accuracy of their answers. The slight bump in confidence at 75% is likely an artifact of the test methodology. The default value of the confidence slider (website user interface element) was 75%. On clicking the Submit button, users were warned if most of their responses specified the default value, but an acquiescence effect appears to have present anyway. In Superforecasters Philip Tetlock observed that many people seem to have a “three settings” (yes, no, maybe) mindset about matters of probability. That could also explain the slight peak at 75%.
I’ve been using a similar approach to confidence calibration in group decision settings for the past three decades. I learned it from a DoD publication by Sarah Lichtenstein and Baruch Fischhoff while working on the Midgetman Small Intercontinental Ballistic Missile program in the mid 1980s. Doug Hubbard teaches a similar approach in his book The Failure of Risk Management. In my experience with diverse groups contributing to risk analysis, where group decisions about likelihood of uncertain events are needed, an hour of training using similar tools yields impressive improvements in calibration as measured above.
Risk Neutrality and Corporate Risk Frameworks
Posted by Bill Storage in Uncategorized on October 27, 2020
Wikipedia describes risk-neutrality in these terms: “A risk neutral party’s decisions are not affected by the degree of uncertainty in a set of outcomes, so a risk-neutral party is indifferent between choices with equal expected payoffs even if one choice is riskier”
While a useful definition, it doesn’t really help us get to the bottom of things since we don’t all remotely agree on what “riskier” means. Sometimes, by “risk,” we mean an unwanted event: “falling asleep at the wheel is one of the biggest risks of nighttime driving.” Sometimes we equate “risk” with the probability of the unwanted event: “the risk of losing in roulette is 35 out of 36. Sometimes we mean the statistical expectation. And so on.
When the term “risk” is used in technical discussions, most people understand it to involve some combination of the likelihood (probability) and cost (loss value) of an unwanted event.
We can compare both the likelihoods and the costs of different risks, but deciding which is “riskier” using a one-dimensional range (i.e., higher vs. lower) requires a scalar calculus of risk. If risk is a combination of probability and severity of an unwanted outcome, riskier might equate to a larger value of the arithmetic product of the relevant probability (a dimensionless number between zero and one) and severity, measured in dollars.
But defining risk as such a scalar (area under the curve, therefore one dimensional) value is a big step, one that most analyses of human behavior suggests is not an accurate representation of how we perceive risk. It implies risk-neutrality.
Most people agree, as Wikipedia states, that a risk-neutral party’s decisions are not affected by the degree of uncertainty in a set of outcomes. On that view, a risk-neutral party is indifferent between all choices having equal expected payoffs.
Under this definition, if risk-neutral, you would have no basis for preferring any of the following four choices over another:
1) a 50% chance of winning $100.00
2) An unconditional award of $50.
3) A 0.01% chance of winning $500,000.00
4) A 90% chance of winning $55.56.
If risk-averse, you’d prefer choices 2 or 4. If risk-seeking, you’d prefer 1 or 3.
Now let’s imagine, instead of potential winnings, an assortment of possible unwanted events, termed hazards in engineering, for which we know, or believe we know, the probability numbers. One example would be to simply turn the above gains into losses:
1) a 50% chance of losing $100.00
2) An unconditional payment of $50.
3) A 0.01% chance of losing $500,000.00
4) A 90% chance of losing $55.56.
In this example, there are four different hazards. Many argue that rational analysis of risk entails quantification of hazard severities, independent of whether their probabilities are quantified. Above we have four risks, all having the same $50 expected value (cost), labeled 1 through 4. Whether those four risks can be considered equal depends on whether you are risk-neutral.
If forced to accept one of the four risks, a risk-neutral person would be indifferent to the choice; a risk seeker might choose risk 3, etc. Banks are often found to be risk-averse. That is, they will pay more to prevent risk 3 than to prevent risk 4, even though they have the same expected value. Viewed differently, banks often pay much more to prevent one occurrence of hazard 3 (cost = $500,000) than to prevent 9000 occurrences of hazard 4 (cost = $500,000).
Businesses compare risks to decide whether to reduce their likelihood, to buy insurance, or to take other actions. They often use a heat-map approach (sometimes called risk registers) to visualize risks. Heat maps plot probability vs severity and view any particular risk’s riskiness as the area of the rectangle formed by the axes and the point on the map representing that risk. Lines of constant risk therefore look like y = 1 / x. To be precise, they take the form of y = a/x where a represents a constant number of dollars called the expected value (or mathematical expectation or first moment) depending on area of study.
By plotting the four probability-cost vector values (coordinates) of the above four risks, we see that they all fall on the same line of constant risk. A sample curve of this form, representing a line of constant risk appears below on the left.
In my example above, the four points (50% chance of losing $100, etc.) have a large range of probabilities. Plotting these actual values on a simple grid isn’t very informative because the data points are far from the part of the plotted curve where the bend is visible (plot below on the right).
Students of high-school algebra know the fix for the problem of graphing data of this sort (monomials) is to use log paper. By plotting equations of the form described above using logarithmic scales for both axes, we get a straight line, having data points that are visually compressed, thereby taming the large range of the data, as below.
The risk frameworks used in business take a different approach. Instead of plotting actual probability values and actual costs, they plot scores, say from one ten. Their reason for doing this is more likely to convert an opinion into a numerical value than to cluster data for easy visualization. Nevertheless, plotting scores – on linear, not logarithmic, scales – inadvertently clusters data, though the data might have lost something in the translation to scores in the range of 1 to 10. In heat maps, this compression of data has the undesirable psychological effect of implying much small ranges for the relevant probability values and costs of the risks under study.
A rich example of this effect is seen in the 2002 PmBok (Project Management Body of Knowledge) published by the Project Management Institute. It assigns a score (which it curiously calls a rank) of 10 for probability values in the range of 0.5, a score of 9 for p=0.3, and a score of 8 for p=0.15. It should be obvious to most having a background in quantified risk that differentiating failure probabilities of .5, .3, and .15 is pointless and indicative of bogus precision, whether the probability is drawn from observed frequencies or from subjectivist/Bayesian-belief methods.
The methodological problem described above exists in frameworks that are implicitly risk-neutral. The real problem with the implicit risk-neutrality of risk frameworks is that very few of us – individuals or corporations – are risk-neutral. And no framework is right to tell us that we should be. Saying that it is somehow rational to be risk-neutral pushes the definition of rationality too far.
As proud king of a small distant planet of 10 million souls, you face an approaching comet that, on impact, will kill one million (10%) in your otherwise peaceful world. Your scientists and engineers rush to build a comet-killer nuclear rocket. The untested device has a 90% chance of destroying the comet but a 10% chance of exploding on launch thereby killing everyone on your planet. Do you launch the comet-killer, knowing that a possible outcome is total extinction? Or do you sit by and watch one million die from a preventable disaster? Your risk managers see two choices of equal riskiness: 100% chance of losing one million and a 10% chance of losing 10 million. The expected value is one million lives in both cases. But in that 10% chance of losing 10 million, there is no second chance. It’s an existential risk.
If these two choices seem somehow different, you are not risk-neutral. If you’re tempted to leave problems like this in the capable hands of ethicists, good for you. But unaware boards of directors have left analogous dilemmas in the incapable hands of simplistic and simple-minded risk frameworks.
The risk-neutrality embedded in risk frameworks is a subtle and pernicious case of Hume’s Guillotine – an inference from “is” to “ought” concealed within a fact-heavy argument. No amount of data, whether measured frequencies or subjective probability estimates, whether historical expenses or projected costs, even if recorded as PmBok’s scores and ranks, can justify risk-neutrality to parties who are not risk-neutral. So why is it embed it in the frameworks our leading companies pay good money for?
The Dose Makes the Poison
Posted by Bill Storage in Uncategorized on October 19, 2020
Toxicity is binary in California. Or so says its governor and most of its residents.
Governor Newsom, who believes in science, recently signed legislation making California the first state to ban 24 toxic chemicals in cosmetics.
The governor’s office states “AB 2762 bans 24 toxic chemicals in cosmetics, which are linked to negative long-term health impacts especially for women and children.”
The “which” in that statement is a nonrestrictive pronoun, and the comma preceding it makes the meaning clear. The sentence says that all toxic chemicals are linked to health impacts and that AB 2762 bans 24 of them – as opposed to saying 24 chemicals that are linked to health effects are banned. One need not be a grammarian or George Orwell to get the drift.
California continues down the chemophobic path, established in the 1970s, of viewing all toxicity through the beloved linear no-threshold lens. That lens has served gullible Californians well since the 1974, when the Sierra Club, which had until then supported nuclear power as “one of the chief long-term hopes for conservation,” teamed up with the likes of Gov. Jerry Brown (1975-83, 2011-19) and William Newsom – Gavin’s dad, investment manager for Getty Oil – to scare the crap out of science-illiterate Californians about nuclear power.
That fear-mongering enlisted Ralph Nadar, Paul Ehrlich and other leading Malthusians, rock stars, oil millionaires and overnight-converted environmentalists. It taught that nuclear plants could explode like atom bombs, and that anything connected to nuclear power was toxic – in any dose. At the same time Governor Brown, whose father had deep oil ties, found that new fossil fuel plants could be built “without causing environmental damage.” The Sierra Club agreed, and secretly took barrels of cash from fossil fuel companies for the next four decades – $25M in 2007 from subsidiaries of, and people connected to, Chesapeake Energy.
What worked for nuclear also works for chemicals. “Toxic chemicals have no place in products that are marketed for our faces and our bodies,” said First Partner Jennifer Siebel Newsom in response to the recent cosmetics ruling. Jennifer may be unaware that the total amount of phthalates in the banned zipper tabs would yield very low exposure indeed.
Chemicals cause cancer, especially in California, where you cannot enter a parking garage, nursery, or Starbucks without reading a notice that the place can “expose you to chemicals known to the State of California to cause birth defects.” California’s litigator-lobbied legislators authored Proposition 65 in a way that encourages citizens to rat on violators, the “citizen enforcers” receiving 25% of any penalties assessed by the court. The proposition lead chemophobes to understand that anything “linked to cancer” causes cancer. It exaggerates theoretical cancer risks stymying the ability of the science-ignorant educated class to make reasonable choices about actual risks like measles and fungus.
California’s linear no-threshold conception of chemical carcinogens actually started in 1962 with Rachel Carson’s Silent Spring, the book that stopped DDT use, saving all the birds, with the minor side effect of letting millions of Africans die of malaria who would have survived (1, 2, 3) had DDT use continued.
But ending DDT didn’t save the birds, because DDT wasn’t the cause of US bird death as Carson reported, because the bird death at the center of her impassioned plea never happened. This has been shown by many subsequent studies; and Carson, in her work at Fish and Wildlife Service and through her participation in Audubon bird counts, certainly had access to data showing that the eagle population doubled, and robin, catbird, and dove counts had increased by 500% between the time DDT was introduced and her eloquence, passionate telling of the demise of the days that once “throbbed with the dawn chorus of robins, catbirds, and doves.”
Carson also said that increasing numbers of children were suffering from leukemia, birth defects and cancer, and of “unexplained deaths,” and that “women were increasingly unfertile.” Carson was wrong about increasing rates of these human maladies, and she lied about the bird populations. Light on science, Carson was heavy on influence: “Many real communities have already suffered.”
In 1969 the Environmental Defense Fund demanded a hearing on DDT. Lasting eight months, the examiner’s verdict concluded DDT was not mutagenic or teratogenic. No cancer, no birth defects. In found no “deleterious effect on freshwater fish, estuarine organisms, wild birds or other wildlife.”
William Ruckleshaus, first director of the EPA didn’t attend the hearings or read the transcript. Pandering to the mob, he chose to ban DDT in the US anyway. It was replaced by more harmful pesticides in the US and the rest of the world. In praising Ruckleshaus, who died last year, NPR, the NY Times and the Puget Sound Institute described his having a “preponderance of evidence” of DDT’s damage, never mentioning the verdict of that hearing.
When Al Gore took up the cause of climate, he heaped praise on Carson, calling her book “thoroughly researched.” Al’s research on Carson seems of equal depth to Carson’s research on birds and cancer. But his passion and unintended harm have certainly exceeded hers. A civilization relying on the low-energy-density renewables Gore advocates will consume somewhere between 100 and 1000 times more space for food and energy than we consume at present.
California’s fallacious appeal to naturalism regarding chemicals also echoes Carson’s, and that of her mentor, Wilhelm Hueper, who dedicated himself to the idea that cancer stemmed from synthetic chemicals. This is still overwhelmingly the sentiment of Californians, despite the fact that the smoking-tar-cancer link now seems a bit of a fluke. That is, we expected the link between other “carcinogens” and cancer to be as clear as the link between smoking and cancer. It is not remotely. As George Johnson, author of The Cancer Chronicles, wrote, “as epidemiology marches on, the link between cancer and carcinogen seems ever fuzzier” (re Tomasetti on somatic mutations). Carson’s mentor Hueper, incidentally, always denied that smoking caused cancer, insisting toxic chemicals released by industry caused lung cancer.
This brings us back to the linear no-threshold concept. If a thing kills mice in high doses, then any dose to humans is harmful – in California. And that’s accepting that what happens in mice happens in humans, but mice lie and monkeys exaggerate. Outside California, most people are at least aware of certain hormetic effects (U-shaped dose-response curve). Small amounts of Vitamin C prevent scurvy; large amounts cause nephrolithiasis. Small amounts of penicillin promote bacteria growth; large amount kill them. There is even evidence of biopositive effects from low-dose radiation, suggesting that 6000 millirems a year might be best for your health. The current lower-than-baseline levels of cancers in 10,000 residents of Taiwan accidentally exposed to radiation-contaminated steel, in doses ranging from 13 to 160 mSv/yr for ten years starting in 1982 is a fascinating case.
Radiation aside, perpetuating a linear no-threshold conception of toxicity in the science-illiterate electorate for political reasons is deplorable, as is the educational system that produces degreed adults who are utterly science-illiterate – but “believe in science” and expect their government to dispense it responsibly. The Renaissance physician Paracelsus knew better half a millennium ago when he suggested that that substances poisonous in large doses may be curative in small ones, writing that “the dose makes the poison.”
To demonstrate chemophobia in 2003, Penn Jillette and assistant effortlessly convinced people in a beach community, one after another, to sign a petition to ban dihydrogen monoxide (H2O). Water is of course toxic in high doses, causing hyponatremia, seizures and brain damage. But I don’t think Paracelsus would have signed the petition.


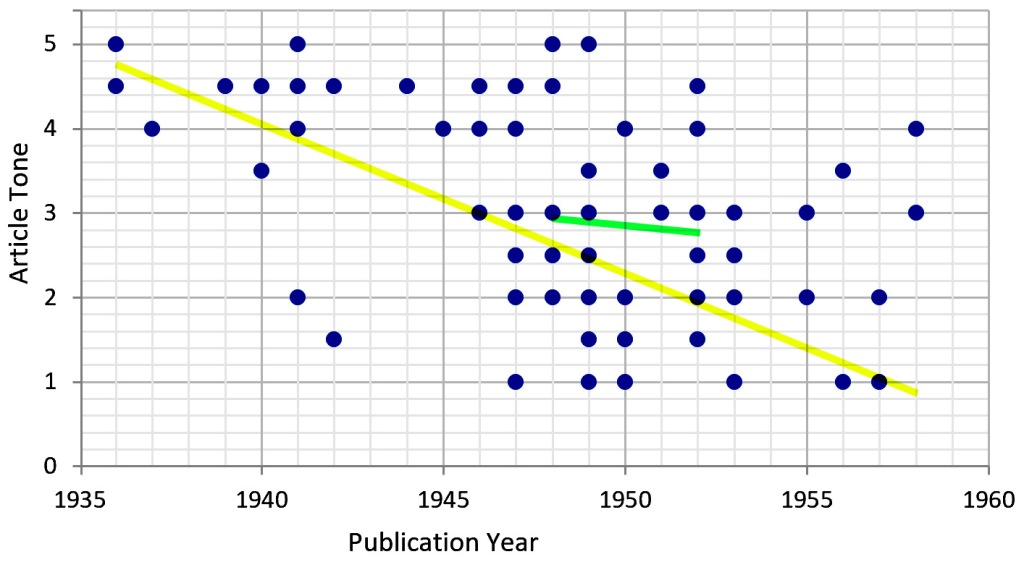


Recent Comments